题目内容
【题目】如图1，直线
将矩形纸
分为两个直角梯形
和
，将梯形沿边翻折，如图2，在翻折的过程中（平面和平面不重合），下面说法正确的是
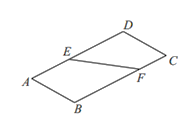
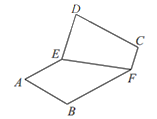
图1 图2
A.存在某一位置，使得
平面
B.存在某一位置，使得
平面
C.在翻折的过程中，
平面
恒成立
D.在翻折的过程中，
平面恒成立
【答案】C
【解析】
因为
与
相交，所以与平面
相交，故A错误.
在任何位置都不垂直于，如果“存在某一位置，使得
平面”，则存在某一位置，使得
，两者矛盾，故B错误.
在任何位置都不垂直于，如果“在翻折的过程中，
平面
恒成立”，那么
恒成立，两者矛盾，故D错误.
由题意知与不平行，且在同一平面内.
所以，与相交，所以与平面相交，故A错误.
在任何位置都不垂直于，如果“存在某一位置，使得平面”，则存在某一位置，使得，两者矛盾，故B错误.
在任何位置都不垂直于，如果“在翻折的过程中，平面恒成立”，那么恒成立，两者矛盾，故D错误.
综上，选C.
练习册系列答案
名校课堂系列答案
相关题目
