Question

求经过点P(-3，0)、Q(0，2)的椭圆的标准方程.

Answer 1

思路分析：本题主要考查用待定系数法求椭圆的标准方程，已知椭圆方程上的两个点，要求出椭圆的方程，可以合理设式，从而代值计算.

解：设椭圆的标准方程为mx²+ny²=1(m＞0,n＞0,m≠n).

∵椭圆经过点P(-3，0)和Q(0，2)，

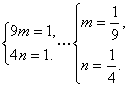∴.∴所求椭圆方程为.

    方法归纳 在求椭圆的标准方程时必须先判断焦点的位置然后再设出方程.在无法判断焦点的位置时可设mx²+ny²=1(m＞0，n＞0，m≠n)，而不规定m与n的大小关系，从而避免去讨论焦点位置.