题目内容
已知数列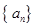 的前
的前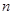 项和
项和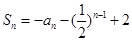 (
(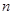 为正整数)。
为正整数)。
(1) 令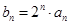 ,求证:数列
,求证:数列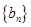 是等差数列,并求数列
是等差数列,并求数列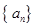 的通项公式;
的通项公式;
(2) 令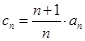 ,
,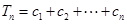 ,求使得
,求使得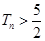 成立的最小正整数
成立的最小正整数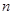 ,并证明你的结论.
,并证明你的结论.
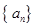 的前
的前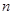 项和
项和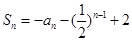 (
(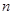 为正整数)。
为正整数)。(1) 令
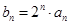 ,求证:数列
,求证:数列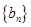 是等差数列,并求数列
是等差数列,并求数列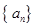 的通项公式;
的通项公式;(2) 令
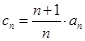 ,
,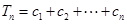 ,求使得
,求使得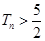 成立的最小正整数
成立的最小正整数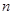 ,并证明你的结论.
,并证明你的结论.(1)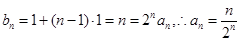
(2)最小正整数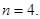
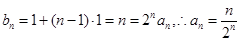
(2)最小正整数
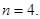
试题分析:解:(1)在
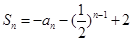 中,
中,令n=1,可得
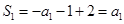 ,即
,即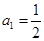 2分
2分当
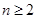 时,
时,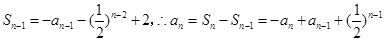 ,
,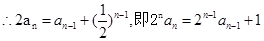 . 2分
. 2分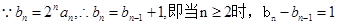 .
.又
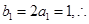 数列
数列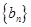 是首项和公差均为1的等差数列. 5分
是首项和公差均为1的等差数列. 5分于是
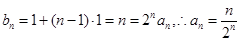 . 7分
. 7分(2)由(1)得
 ,所以
,所以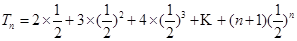
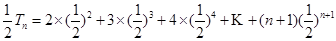 9分
9分由①-②得
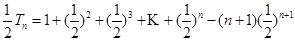
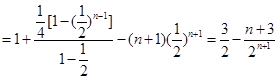
∴
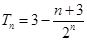 11分
11分∴
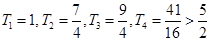 13分
13分下面证明数列
 是递增数列.
是递增数列.∵
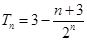 , ∴
, ∴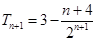 ,
,∴
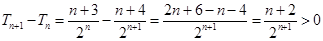 ,
, ∴数列
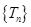 单调递增
单调递增所以, 使得
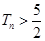 成立的最小正整数
成立的最小正整数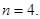 16分
16分点评:主要是考查了等比数列的求和的运用,属于基础题。

练习册系列答案
相关题目
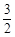 的等比数列
的等比数列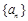 的前n项和为
的前n项和为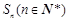 , 且
, 且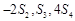 成等差数列.
成等差数列. 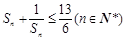 .
. 
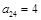 ,
,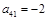 ,
,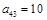 ,则
,则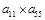 的值为__________
的值为__________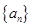 中,已知
中,已知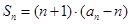 (
(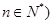 .
.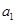 及
及 ;
;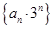 的前
的前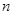 项和
项和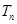 .
.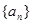 的前n项和为
的前n项和为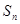 , 公差为d, 已知
, 公差为d, 已知
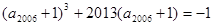 , 则下列结论正确的是 ( )
, 则下列结论正确的是 ( )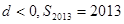
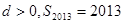
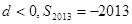
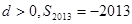
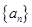 中,已知
中,已知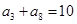 ,则
,则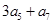
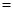 _____.
_____.
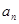 }的前21项的和等于前8项的和.若
}的前21项的和等于前8项的和.若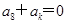 ,则k=( )
,则k=( )