题目内容
已知a,b为实数,则“a≥b”是“a3≥b3”的( )
| A、既不充分又不必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、充要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质结合充分条件和必要条件的定义即可得到结论.
解答:
解:∵函数f(x)=x3,在定义域上是增函数,
∴“a≥b”是“a3≥b3”的充要条件,
故选:D
∴“a≥b”是“a3≥b3”的充要条件,
故选:D
点评:本题主要考查充分条件和必要条件的判断,根据函数的单调性的性质是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知a=21.2,b=(
)-0.2,c=2log52,则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |
已知函数f(x)=|x-1|,则下列函数与f(x)相等的函数是( )
A、g(x)=
| |||||||
B、g(x)=
| |||||||
C、g(x)=
| |||||||
| D、g(x)=x-1 |
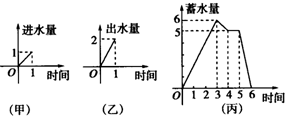 水池有两个相同的进水口和一个出水口,每个口进出水速度如下图(甲)、(乙)所示,某天0点到6点该水池蓄水量如图(丙)所以(至少打开一个水口)给出以下3个论断:
水池有两个相同的进水口和一个出水口,每个口进出水速度如下图(甲)、(乙)所示,某天0点到6点该水池蓄水量如图(丙)所以(至少打开一个水口)给出以下3个论断: