题目内容
设关于![]() 的方程
的方程![]()
(Ⅰ)若方程有实数解,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个数,并求出方程的解.
解:(Ⅰ)原方程为![]() ,
,
![]() ,
,
![]() 时方程有实数解;-------------------------4分
时方程有实数解;-------------------------4分
(Ⅱ)①当![]() 时,
时,![]() ,∴方程有唯一解
,∴方程有唯一解![]() ;----6分
;----6分
②当![]() 时,
时,![]() .
.
![]() 的解为
的解为![]() ;--8分
;--8分
令![]()
![]() 的解为
的解为![]() ;--10分
;--10分
综合①、②,得
1)当![]() 时原方程有两解:
时原方程有两解:![]() ;
;
2)当![]() 时,原方程有唯一解
时,原方程有唯一解![]() ;-------12分
;-------12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
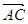 =(
=(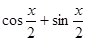 ,
,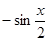 ),
),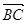 =(
=(
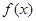 =
=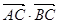 (1)求
(1)求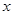 的方程
的方程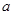 在[
在[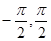 ]有两个不相等的实数根,求
]有两个不相等的实数根,求 的方程
的方程
 的取值范围;
的取值范围;