题目内容
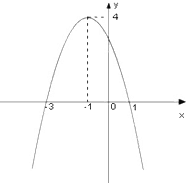 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.(1)写出f(x)>0的解集;
(2)求这个二次函数的解析式;
(3)当实数k在何范围内变化时,g(x)=f(x)-kx在区间[-2,2]上是单调函数.
分析:(1)由图可知二次函数的零点为-3和1,结合已知函数的图象可写出不等式的解集
(2)设二次函数为y=a(x+3)(x-1)a≠0,由点(-1,4)在函数图象上,可求a
(3)由题意可得,g(x)=-x2-2x+3-kx=-x2-(k+2)x+3口向下,对称轴为x=-
,结合对称轴相对应区间[-2,2]的位置,讨论其单调性,可求k的范围
(2)设二次函数为y=a(x+3)(x-1)a≠0,由点(-1,4)在函数图象上,可求a
(3)由题意可得,g(x)=-x2-2x+3-kx=-x2-(k+2)x+3口向下,对称轴为x=-
| k+2 |
| 2 |
解答:解:(1)由图可知二次函数的零点为-3和1
注:若零点写为(-3,0),(2,0),则不给分
(2)设二次函数为y=a(x+3)(x-1)a≠0,
由点(-1,4)在函数图象上,得a=-1
所以二次函数的解析式为y=-(x+3)(x-1)=-x2-2x++3.
(3)g(x)=-x2-2x+3-kx=-x2-(k+2)x+3口向下,
对称轴为x=-
当-
≤-2即k≥2时g(x)在[-2,2]上单调递减
当-
≥2即k≤-6时,g(x)在[-2,2]上单调递增
综上可得,k≤-6或k≥2
注:若零点写为(-3,0),(2,0),则不给分
(2)设二次函数为y=a(x+3)(x-1)a≠0,
由点(-1,4)在函数图象上,得a=-1
所以二次函数的解析式为y=-(x+3)(x-1)=-x2-2x++3.
(3)g(x)=-x2-2x+3-kx=-x2-(k+2)x+3口向下,
对称轴为x=-
| k+2 |
| 2 |
当-
| k+2 |
| 2 |
当-
| k+2 |
| 2 |
综上可得,k≤-6或k≥2
点评:本题主要考查了二次函数解析式的求解及二次函数的性质的应用,解题的关键是熟练掌握基本性质

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象. 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.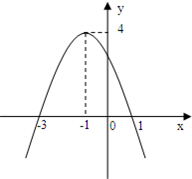 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象