题目内容
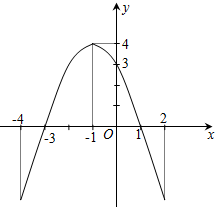 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.(1)写出这个二次函数的零点;
(2)写出这个二次函数的解析式;
(3)当x∈[-4,0]时,仔细观察图象,直接写出函数的值域.
分析:(1)根据图象得到函数与x轴的交点坐标,从而确定函数的零点.
(2)根据二次函数的顶点坐标和对称轴以及函数过点(0,3),联立得到函数的解析式,.
(3)根据图象确定函数的值域.
(2)根据二次函数的顶点坐标和对称轴以及函数过点(0,3),联立得到函数的解析式,.
(3)根据图象确定函数的值域.
解答:解:(1)由图象可知函数的两个零点为x1=-3,x2=1.
(2)由图象可知二次函数的对称轴为x=-1,顶点坐标为(-1,4),
所以二次函数的解析式为f(x)=a(x+1)2+4,因为函数过点(0,3),所以代入解得a=-1,
所以二次函数的解析式为f(x)=-x2-2x+3.
(3)由图象可知,当x=-1时,函数有最大值4,当x=-4时,函数有最小值-5,
所以函数的值域是[-5,4].
(2)由图象可知二次函数的对称轴为x=-1,顶点坐标为(-1,4),
所以二次函数的解析式为f(x)=a(x+1)2+4,因为函数过点(0,3),所以代入解得a=-1,
所以二次函数的解析式为f(x)=-x2-2x+3.
(3)由图象可知,当x=-1时,函数有最大值4,当x=-4时,函数有最小值-5,
所以函数的值域是[-5,4].
点评:本题主要考查二次函数的图象和性质,比较基础.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
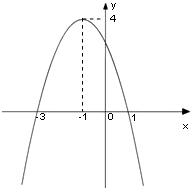 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象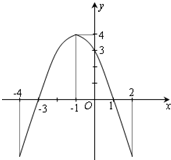 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.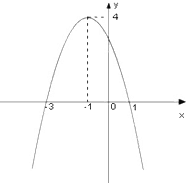 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.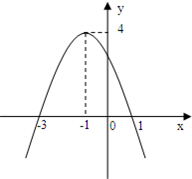 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象