题目内容
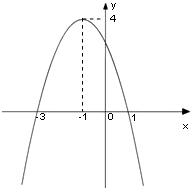 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象(1)写出这个二次函数的零点
(2)求这个二次函数的解析式
(3)当实数k在何范围内变化时,函数g(x)=f(x)-kx在区间[-2,2]上是单调函数?
分析:(1)根据图象,找函数图象与横轴交点的横坐标即可.
(2)由顶点是(-1,4)可设函数为:y=a(x+1)2+4,再代入(-3,0)即可.
(3)先化简函数g(x)=-x2-2x+3-kx=-x2-(k+2)x+3易知图象开口向下,对称轴为x=-
,因为是单调,则对称轴在区间的两侧求解即可.
(2)由顶点是(-1,4)可设函数为:y=a(x+1)2+4,再代入(-3,0)即可.
(3)先化简函数g(x)=-x2-2x+3-kx=-x2-(k+2)x+3易知图象开口向下,对称轴为x=-
| k+2 |
| 2 |
解答:解:(1)由图可知,此二次函数的零点是-3,1
(2)∵顶点是(-1,4)
∴设函数为:y=a(x+1)2+4,
∵(-3,0)在图象上
∴a=-1
∴函数为y=-x2-2x+3
(3)∵g(x)=-x2-2x+3-kx=-x2-(k+2)+3
∴图象开口向下,对称轴为x=-
当-
≤-2,即k≥2时,g(x)在[-2,2]上是减函数
当-
≥2,即k≤-6时,g(x)在[-2,2]上是增函数
综上所述k≤-6或k≥2时,g(x)在[-2,2]上是单调函数
(2)∵顶点是(-1,4)
∴设函数为:y=a(x+1)2+4,
∵(-3,0)在图象上
∴a=-1
∴函数为y=-x2-2x+3
(3)∵g(x)=-x2-2x+3-kx=-x2-(k+2)+3
∴图象开口向下,对称轴为x=-
| k+2 |
| 2 |
当-
| k+2 |
| 2 |
当-
| k+2 |
| 2 |
综上所述k≤-6或k≥2时,g(x)在[-2,2]上是单调函数
点评:本题主要考查二次函数的零点,解析式的求法及单调性的研究.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
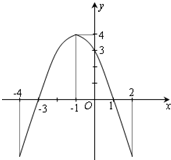 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.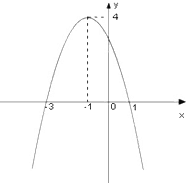 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.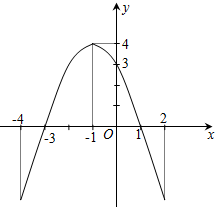 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.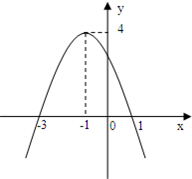 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象