题目内容
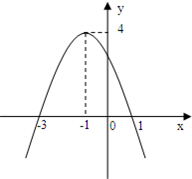 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象(1)写出这个二次函数的零点,并求这个二次函数的解析式;
(2)设函数g(x)=
| f(x)+2x | x |
分析:(1)由y=f(x)的图象得出零点,求出解析式;
(2)用单调性定义证明g(x)在区间(0,+∞)上是减函数.
(2)用单调性定义证明g(x)在区间(0,+∞)上是减函数.
解答:解:(1)由图象知,y=f(x)的图象与x轴交点为(-3,0),(1,0),
∴y=f(x)的零点是x=-3和x=1;
设y=f(x)=a(x+3)(x-1),图象过点(-1,4),
∴a(-1+3)(-1-1)=4,
解得a=-1,
∴y=f(x)=-(x+3)(x-1)=-x2-2x+3;
(2)g(x)在区间(0,+∞)上是减函数,证明:
∵f(x)=-x2-2x+3;
∴g(x)=
=
=-x+
,
在(0,+∞)上任取x1,x2,且x1<x2,
则g(x1)-g(x2)=(-x1+
)-(-x2+
)=(x2-x1)+
=
;
∵0<x1<x2,
∴x2-x1>0,x1x2>0,
∴g(x1)>g(x2);
∴g(x)在区间(0,+∞)上是减函数.
∴y=f(x)的零点是x=-3和x=1;
设y=f(x)=a(x+3)(x-1),图象过点(-1,4),
∴a(-1+3)(-1-1)=4,
解得a=-1,
∴y=f(x)=-(x+3)(x-1)=-x2-2x+3;
(2)g(x)在区间(0,+∞)上是减函数,证明:
∵f(x)=-x2-2x+3;
∴g(x)=
| f(x)+2x |
| x |
| -x2-2x+3+2x |
| x |
| 2 |
| x |
在(0,+∞)上任取x1,x2,且x1<x2,
则g(x1)-g(x2)=(-x1+
| 2 |
| x1 |
| 2 |
| x2 |
| 2(x2-x1) |
| x1x2 |
| (x2-x1)(x1x2+2) |
| x1x2 |
∵0<x1<x2,
∴x2-x1>0,x1x2>0,
∴g(x1)>g(x2);
∴g(x)在区间(0,+∞)上是减函数.
点评:本题考查了利用函数的图象求解析式以及函数单调性的判定问题,是基础题.

练习册系列答案
相关题目
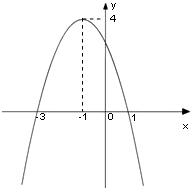 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象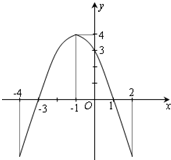 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.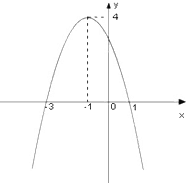 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.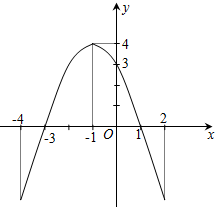 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象.