题目内容
已知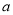 是大于0的实数,函数
是大于0的实数,函数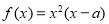 .
.
(Ⅰ)若曲线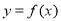 在点
在点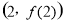 处的切线平行与X轴,求
处的切线平行与X轴,求 值;
值;
(Ⅱ)求 在区间
在区间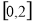 上的最小值;
上的最小值;
(III)在(Ⅰ)的条件下,设 是
是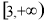 上的增函数,求实数
上的增函数,求实数 的最大值。
的最大值。
(Ⅰ)
(Ⅱ) 时,
时,
 时,
时,
(III)36
【解析】
试题分析:解决该题的关键是应用导数的几何意义,得出切线的斜率为0,从而得出
 ,从而得出a所满足的等量关系式,从而求出参数的值,关于函数在某个闭区间上的最值问题得需要讨论函数在相应的区间上的单调性,要对参数的值进项讨论,函数满足单调增,可以应用函数的导数在给定区间上满足非负恒成立即可求得.
,从而得出a所满足的等量关系式,从而求出参数的值,关于函数在某个闭区间上的最值问题得需要讨论函数在相应的区间上的单调性,要对参数的值进项讨论,函数满足单调增,可以应用函数的导数在给定区间上满足非负恒成立即可求得.
试题解析:(Ⅰ) , 1分
, 1分
因为 ,所以
,所以 . 3分
. 3分
(Ⅱ)令 ,解得
,解得 ,
, . 5分
. 5分
①当 ,即
,即 时,
时, 在
在 上单调递减,从而
上单调递减,从而 6分
6分
②当 ,即
,即 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,从而
上单调递增,从而 7分
7分
综上所述,
 时,
时,
 时,
时, 8分
8分
(III)由(Ⅰ)得 ,所以
,所以
 ,
,  9分
9分
∵ 是
是 上的增函数,∴
上的增函数,∴ 在
在 上恒成立,
上恒成立,
即 在
在 上恒成立。 10分
上恒成立。 10分
设 ∴
∴ 上恒成立。
上恒成立。
∴ 在
在 上恒成立 12分
上恒成立 12分
令
∴ ∴实数
∴实数 的最大值是36。 14分
的最大值是36。 14分
考点:导数的几何意义,函数在某个闭区间上的最值问题,根据函数的单调性确定参数的值.

练习册系列答案
相关题目
 为纯虚数,
为纯虚数, 是虚数单位,则实数
是虚数单位,则实数 的值是 .
的值是 . ,
, ,且
,且 在区间
在区间 上递减,则
上递减,则 ( )
( ) 中, 点
中, 点 关于原点
关于原点 的对称点的坐标为 .
的对称点的坐标为 .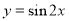 是( )
是( )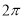 的偶函数
的偶函数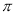 的偶函数
的偶函数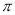 的奇函数
的奇函数 :
: ;命题
;命题 :
: 解集非空.
解集非空. ,求
,求 的取值范围.
的取值范围.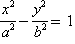 (a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有
(a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有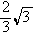 ) C.[2,+∞) D.[
) C.[2,+∞) D.[ 是以
是以 为直角顶点的等腰直角三角形,其中
为直角顶点的等腰直角三角形,其中 ,
, (
( ),则
),则
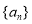 是递增的等差数列,
是递增的等差数列,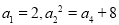 .
.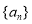 的通项公式;
的通项公式;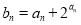 ,求数列
,求数列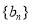 的前n项和
的前n项和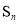 .
.