题目内容
13.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2$\sqrt{3}$,b=$\sqrt{6}$,A=45°,那么角B的值为30°.分析 由已知及正弦定理可得sinB=$\frac{1}{2}$,利用大边对大角可求B为锐角,利用特殊角的三角函数值即可得解B的值.
解答 解:在△ABC中,∵a=2$\sqrt{3}$,b=$\sqrt{6}$,A=45°,
∴由正弦定理可得:sinB=$\frac{b•sinA}{a}$=$\frac{\sqrt{6}×\frac{\sqrt{2}}{2}}{2\sqrt{3}}$=$\frac{1}{2}$,
∵b<a,可得B为锐角,
∴B=30°.
故答案为:30°.
点评 本题主要考查了正弦定理,大边对大角,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
3.若复数z满足$\frac{zi}{z-i}=1$,其中i为虚数单位,则复数z的共轭复数为( )
| A. | $-\frac{1}{2}+\frac{i}{2}$ | B. | $-\frac{1}{2}-\frac{i}{2}$ | C. | $\frac{1}{2}-\frac{i}{2}$ | D. | $\frac{1}{2}+\frac{i}{2}$ |
4.执行如图所示的程序框图,如果输入的a,b分别为56,140,则输出的a=( )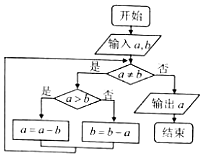

| A. | 0 | B. | 7 | C. | 14 | D. | 28 |
18.在2,0,1,7这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
5.如图是求12+22+32+…+1002的程序框图,则图中的①②分别是( )
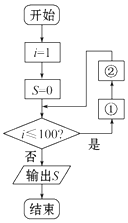

| A. | ①S=S+i ②i=i+1 | B. | ①S=S+i2 ②i=i+1 | C. | ①i=i+1 ②S=S+i | D. | ①i=i+1 ②S=S+i2 |