题目内容
设n=
4sinxdx，则二项式（x-
）n的展开式的常数项是（ ）
| ∫ |
0 |
| 1 |
| x |
| A、12 | B、-2 | C、4 | D、1 |
考点：定积分,二项式系数的性质
专题：二项式定理
分析：由定积分求出n的值，然后直接代入二项式求出常数项．
解答：
解：∵n
4sinxdx=-4cosx
=-4cos
-(-4cos0)=2，
∴（x-
）n=(x-
)2=x2-2+
．
∴二项式（x-
）n的展开式的常数项是-2．
故选：B．
| =∫ |
0 |
| | |
0 |
| π |
| 3 |
∴（x-
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
∴二项式（x-
| 1 |
| x |
故选：B．
点评：本题考查定积分，考查了二项式的展开式，是基础的计算题．
练习册系列答案
相关题目
已知复数z=
，则复数z在复平面内对应的点位于（ ）
| 1+i+i2+i3+…+i 2014 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知复数z=i，
是z的共轭复数，则
=（ ）
. |
| z |
| ||
| z |
| A、1 | B、-i | C、i | D、-1 |
函数f（x）=lg丨x+1丨的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
设α是一个平面，m，n是两条不同的直线，以下命题不正确的是（ ）
| A、若m∥α，n⊥α，则m⊥n |
| B、若m∥α，m⊥n，则n⊥α |
| C、若m⊥α，n⊥α，则m∥n |
| D、若m⊥α，m∥n，则n⊥α |
函数y=
的图象大致是（ ）
| lg|x| |
| x |
A、 |
B、 |
C、 |
D、 |
已知向量
，
满足|
+
|=|
-
|=2|
|=2，则|
+2
|等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、2
| ||
B、
| ||
| C、3 | ||
| D、4 |
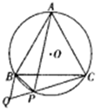如图，圆O是等边三角形ABC的外接圆，点P在劣弧