题目内容
设函数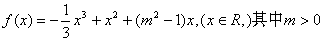
(Ⅰ)当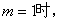 曲线
曲线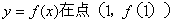 处的切线斜率
处的切线斜率
(Ⅱ)求函数的单调区间与极值;
(Ⅲ)已知函数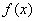 有三个互不相同的零点0,
有三个互不相同的零点0,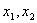 ,且
,且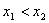 。若对任意的
。若对任意的
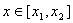 ,
,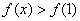 恒成立,求m的取值范围。
恒成立,求m的取值范围。
(1)1(2)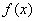 在
在 和
和 内减函数,在
内减函数,在 内增函数。函数
内增函数。函数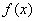 在
在 处取得极大值
处取得极大值 ,且
,且 =
=
函数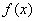 在
在 处取得极小值
处取得极小值 ,且
,且 =
=
解析 解析 当

所以曲线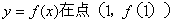 处的切线斜率为1.
处的切线斜率为1.

(2)解析  ,令
,令 ,得到
,得到
因为
当x变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极小值 |
| 极大值 |
|
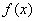 在
在 和
和 内减函数,在
内减函数,在 内增函数。
内增函数。
函数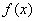 在
在 处取得极大值
处取得极大值 ,且
,且 =
=
函数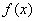 在
在 处取得极小值
处取得极小值 ,且
,且 =
=
(3)解析 由题设, 
所以方程 =0由两个相异的实根
=0由两个相异的实根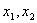 ,故
,故 ,且
,且 ,解得
,解得
因为
若 ,而
,而 ,不合题意
,不合题意
若 则对任意的
则对任意的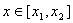 有
有
则 又
又 ,所以函数
,所以函数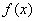 在
在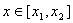 的最小
的最小 值为0,于是对任意的
值为0,于是对任意的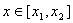 ,
,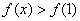 恒成立的充要条件是
恒成立的充要条件是 ,解得
,解得


综上,m的取值范围是

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








 是菱形的四个顶点,求实数
是菱形的四个顶点,求实数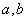 的值.
的值. 的首项为
的首项为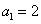 ,公比为
,公比为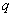 (
(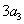 是
是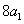 与
与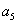 的
的 等差中项;等差数列
等差中项;等差数列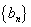 满足
满足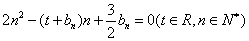 .
.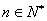 ,有
,有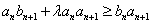 成立,求实数
成立,求实数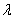 的取值范围;
的取值范围;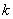 ,在
,在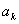 和
和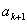 之间插入
之间插入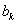 个2,得到一个新数列
个2,得到一个新数列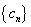 ,设
,设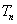 是数列
是数列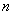 项和,试求满足
项和,试求满足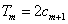 的所有正整数
的所有正整数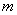 .
.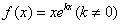
 在点
在点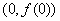 处的切线方程;
处的切线方程;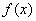 的单调区间;
的单调区间; 内单调递增,求
内单调递增,求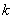 的取值范围.
的取值范围.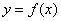 的导函数在区间
的导函数在区间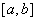 上是增函数,
上是增函数,

 D.
D. ,
, ,且
,且 ,则
,则 的值为 .
的值为 . 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给出下列四个命题:
是两个不重合的平面,给出下列四个命题: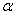 ∥
∥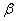 ,
,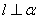 ,则
,则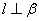 ; ②若
; ②若 ∥
∥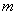 ,
,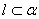 ,
,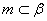 ,则
,则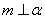 ,
,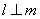 ,则
,则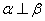 ,
, ,
, ,
, ,
,  ,
, ,猜想第
,猜想第 个等式应为( )
个等式应为( )  B.
B.
 D.
D.
 B.
B.  C.
C.  D.
D. 
