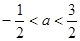题目内容
不等式|2-x|≥1的解集是
| A.{x|1≤x≤3} | B.{x|x≤1或x≥3} |
| C.{x|x≤1} | D.{x|x≥3} |
B
解析试题分析:∵|2-x|≥1,∴2-x≥1或2-x≤1,解得x≤1或x≥3, 故不等式|2-x|≥1的解集是{x|x≤1或x≥3},选B
考点:本题考查了绝对值不等式的解法
点评:解含绝对值不等式的关键是脱掉绝对值符号,有时利用定义,有时利用公式,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若不等式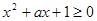 对任意
对任意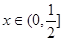 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.0 | B.-2 | C.-3 | D.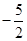 |
不等式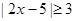 的解集为( )
的解集为( )
A.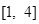 | B.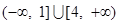 |
C.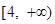 | D.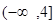 |
若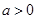 ,使不等式
,使不等式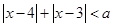 在
在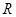 上的解集不是空集的
上的解集不是空集的 的取值是
的取值是
A.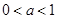 | B.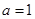 | C.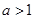 | D.以上均不对 |
已知不等式 >0的解集为(-1,2),
>0的解集为(-1,2),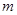 是
是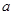 和
和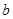 的等比中项,那么
的等比中项,那么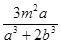 =
=
| A.3 | B.-3 | C.-1 | D.1 |
不等式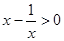 成立的充分不必要条件是( )
成立的充分不必要条件是( )
A.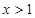 | B.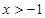 |
C.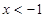 或 或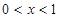 | D.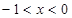 或 或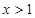 |
已知关于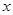 的不等式
的不等式 的解集为
的解集为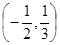 ,则
,则 的值是( )
的值是( )
| A.10 | B.-10 | C.14 | D.-14 |
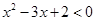 的解集为( )
的解集为( )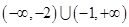 B.
B.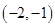
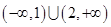 D.
D.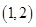
 :x
:x