题目内容
若不等式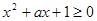 对任意
对任意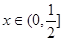 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.0 | B.-2 | C.-3 | D.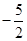 |
D
解析试题分析:根据题意,由于不等式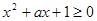 对任意
对任意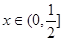 成立,则可知
成立,则可知 ,借助于对勾函数的性质可知,a大于等于函数的在区间
,借助于对勾函数的性质可知,a大于等于函数的在区间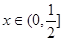 上的最大值即可,即为
上的最大值即可,即为 的最小值为
的最小值为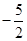 ,故可知答案为D.
,故可知答案为D.
考点:不等式的运用
点评:主要是考查了不等式的求解最值的运用,属于基础题。

练习册系列答案
相关题目
集合 ,
, ,
, ,
, ,则集合
,则集合 的个数为( )
的个数为( )
| A.0 | B.2 | C.4 | D.8 |
对数函数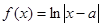 在
在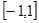 区间上恒有意义,则
区间上恒有意义,则 的取值范围是( )
的取值范围是( )
A.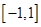 | B.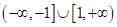 |
C.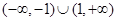 | D.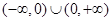 |
下列选项中,使不等式x<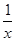 <
<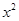 成立的x的取值范围是
成立的x的取值范围是
A.(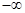 ,-1) ,-1) | B.(-1,0) | C.0,1) | D.(1, 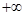 ) ) |
不等式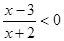 的解集是 ( )
的解集是 ( )
A.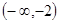 | B.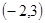 | C. | D. |
若函数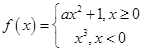 ,则不等式
,则不等式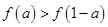 的解集为( )
的解集为( )
A. | B.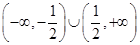 |
C.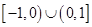 | D.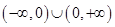 |
设 小于0,则3个数:
小于0,则3个数: ,
,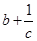 ,
,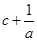 的值 ( )
的值 ( )
| A.至多有一个不小于-2 | B.至多有一个不大于2 |
| C.至少有一个不大于-2 | D.至少有一个不小于2 |
不等式|2-x|≥1的解集是
| A.{x|1≤x≤3} | B.{x|x≤1或x≥3} |
| C.{x|x≤1} | D.{x|x≥3} |



