题目内容
不等式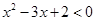 的解集为( )
的解集为( )
A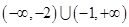 B.
B.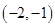
C.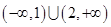 D.
D.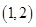
D
解析试题分析:根据已知条件可知,不等式 ,故结合根的大小和开口方向可知解集为
,故结合根的大小和开口方向可知解集为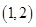 ,选D.
,选D.
考点:一元二次不等式
点评:一元二次不等式的求解,主要是看开口方向以及判别式,结合根的大小来的得到结论,属于基础题。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
不等式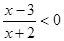 的解集是 ( )
的解集是 ( )
A.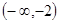 | B.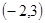 | C. | D. |
已知 ,则2a+3b的取值范围是( )
,则2a+3b的取值范围是( )
A. | B.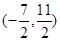 | C. | D.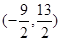 |
设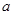 、
、 、
、 是互不相等的正数,现给出下列不等式 ⑴
是互不相等的正数,现给出下列不等式 ⑴ ;⑵
;⑵
 ;⑶
;⑶ ;⑷
;⑷ ,则其中正确个数是( )
,则其中正确个数是( )
| A.0 | B.1 | C.2 | D.3 |
不等式|2-x|≥1的解集是
| A.{x|1≤x≤3} | B.{x|x≤1或x≥3} |
| C.{x|x≤1} | D.{x|x≥3} |
不等式 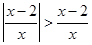 的解集是( )
的解集是( )
A.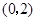 | B.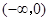 | C.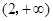 | D.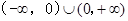 |
当m>1时,关于x的不等式x2+(m-1)x-m≥0的解集是
| A.{x|x≤1,或x≥-m} | B. {x|1≤x≤-m } |
| C.{x|x≤-m,或x≥1} | D. {x|-m≤x≤1 } |
设a、b、c都是正数,则 、
、 、
、 三个数 ( )
三个数 ( )
| A.都大于2 | B.都小于2 |
| C.至少有一个大于2 | D.至少有一个不小于2 |
(文)设x∈R,[x]表示不大于x的最大整数,如:[π]=3,[-1.2]= ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是
A.[2,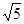 ) ) | B.(-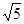 ,-2] ,-2] |
C.(-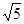 ,-2] ∪[2, ,-2] ∪[2,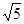 ) ) | D.[-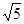 ,-2] ∪[2, ,-2] ∪[2,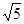 ] ] |