题目内容
7. 河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况汇总成表:
河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况汇总成表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)若从年龄在[55,65),[65,75]的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
分析 (1)利用频率分布直方图中小距形面积之和为1的性质能补全频率分布直方图.
(2)由频率分布直方图得年龄在[55,65),[65,75]的被调查者均有5人,其中赞成“停课”这一举措的分别有3人和4人,由此利用等可能事件概率计算公式能求出这两人都赞成“停课”这一举措的概率.
解答 解:(1)补全频率分布直方图,如下图所示:
(2)年龄在[55,65),[65,75]的被调查者均有0.01×10×50=5人,
其中赞成“停课”这一举措的分别有3人和4人,
从中分别抽取1人的方法数共有:n=5×5=25,
这两人都赞成“停课”这一举措包含的基本事件个数m=3×4=12,
∴这两人都赞成“停课”这一举措的概率p=$\frac{m}{n}=\frac{12}{25}$.
点评 本题考查概率、古典概型等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是基础题.

练习册系列答案
相关题目
18.若z=$\frac{\sqrt{2}}{1-i}$,那么z100的值为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
19.已知x1>0,x1≠1且xn+1=$\frac{{{x_n}(x_n^2+3)}}{3x_n^2+1}$(n=1,2,…).试证:“在数列{xn}中,对任意正整数n都满足xn<xn+1”,当此题用反证法证明,否定结论时,应为( )
| A. | 对任意的正整数n,有xn=xn+1 | B. | 存在正整数n,使xn=xn+1 | ||
| C. | 存在正整数n,使xn≥xn+1 | D. | 存在正整数n,使xn-xn-1≥0 |
17.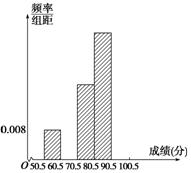 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
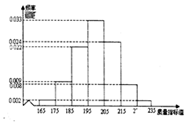 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图: