题目内容
如图所示，在△ABC中，BC边上的两点D、E分别与A连线，假设
，三角形ABC，ABD，ABE的外接圆直径分别为d，e，f，则
- A.d＜f＜e
- B.e＜f＜d
- C.d=e＜f
- D.e=d＞f
D
分析：先由题意可知AD=AC，AE＜AC，再根据正弦定理分别用AD，AC，AE，sinB表示出d，e，f，进而得到答案．
解答：由题意可知，AD=AC，AE＜AC，
根据正弦定理可知：d=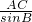
，e=
，f=
，
∴d=e＞f，
故选：D．
点评：本题主要考查了正弦定理在实际中的应用．解决问题的关键在于用AD，AC，AE，sinB表示出d，e，f．
分析：先由题意可知AD=AC，AE＜AC，再根据正弦定理分别用AD，AC，AE，sinB表示出d，e，f，进而得到答案．
解答：由题意可知，AD=AC，AE＜AC，
根据正弦定理可知：d=
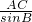，e=，f=，∴d=e＞f，
故选：D．
点评：本题主要考查了正弦定理在实际中的应用．解决问题的关键在于用AD，AC，AE，sinB表示出d，e，f．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在△ABC，已知
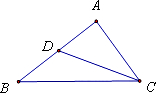如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
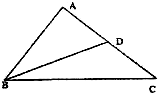如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=
如图所示，在△ABC中，∠BAC=90°，∠ABC=60°，AD⊥BC于D，则
如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=