题目内容
 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则| AD |
分析:先确定点D的位置,然后再根据向量的线性表示用向量
,
表示向量
| AB |
| AC |
| AD |
解答:解:不妨设BD=1,则AB=2,从而由射影定理得:AB2=BD×BC,BC=4
∴点D是BC的靠近点B的一个四等分点,即BD=
BC
∴
=
+
=
+
=
+
(
-
)=
+
故选A
∴点D是BC的靠近点B的一个四等分点,即BD=
| 1 |
| 4 |
∴
| AD |
| AB |
| BD |
| AB |
| 1 |
| 4 |
| BC |
| AB |
| 1 |
| 4 |
| AC |
| AB |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
故选A
点评:本题主要考查向量的线性表示,一般分两步:第一步,把向量表示成一些首尾相接的向量和的形式;第二步,用基底表示这些首尾相接的向量.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
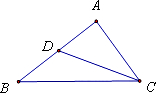 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
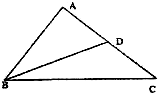 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=