题目内容
 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=| 3 |
分析:以角为测度,计算当BM=1时,∠BAM=30°,再利用几何概型的概率公式求解.
解答:解:由题意,∠B=60°,AD⊥BC,AD=
,可知AB=2,
在△ABM中,利用余弦定理得,当BM=1时,AM2=AB2+BM2-2AB•BMcos∠ABM=4+1-2×2×1×
=3,
∴cos∠BAM=
=
=
,∴∠BAM=30°,
从而所求的概率为P=
=
,
故选B.
| 3 |
在△ABM中,利用余弦定理得,当BM=1时,AM2=AB2+BM2-2AB•BMcos∠ABM=4+1-2×2×1×
| 1 |
| 2 |
∴cos∠BAM=
| AB2+AM2-BM2 |
| 2AB•AM |
| 4+3-1 | ||
2×2×
|
| ||
| 2 |
从而所求的概率为P=
| 30 |
| 180-60-45 |
| 2 |
| 5 |
故选B.
点评:本题主要考查几何概型,正确选择测度是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
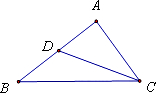 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
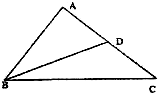 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=