题目内容
已知椭圆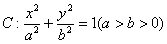 的左右焦点分别是
的左右焦点分别是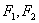 ,离心率
,离心率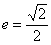 ,
,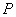 为椭圆上任一点,且
为椭圆上任一点,且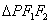 的最大面积为
的最大面积为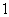 .
.
(Ⅰ)求椭圆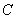 的方程;
的方程;
(Ⅱ)设斜率为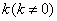 的直线
的直线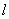 交椭圆
交椭圆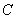 于
于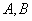 两点,且以
两点,且以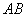 为直径的圆恒过原点
为直径的圆恒过原点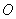 ,若实数
,若实数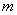 满足条件
满足条件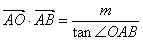 ,求
,求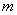 的最大值.
的最大值.
【解】(Ⅰ)依题意得: ,解得:
,解得:
于是:椭圆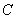 的方程
的方程 
(Ⅱ)设直线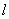
 的方程
的方程 由
由 得:
得:
设 ,则
,则
由于以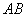 为直径的圆恒过原点
为直径的圆恒过原点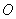 ,于是
,于是 ,
, 即
即
又
于是: ,即
,即
依题意有 :
: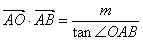 ,即
,即
化简得:
因此,要求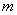 的最大值,只需求
的最大值,只需求 的最大值,下面开始求
的最大值,下面开始求 的最大值:
的最大值:


点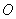 到直线
到直线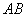 的距离
的距离 ,于是:
,于是:

又因为 ,
, 所以
所以 ,
,
代入得
令
于是:
当 即
即 ,即
,即 时,
时, 取最大值,且最大值为
取最大值,且最大值为
于是: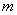 的最大值为
的最大值为

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 表示双曲线,则
表示双曲线,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. 近线方程为y=x,且过点(2,4)的双曲线标准方程为__
近线方程为y=x,且过点(2,4)的双曲线标准方程为__  上的函数
上的函数 ,对任意
,对任意 ,都有
,都有 成立,若函数
成立,若函数 的图象关于点
的图象关于点 对称,则
对称,则 =( )
=( ) 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
. ;
; ,
, ,且
,且 ,求
,求 .
.
 与抛物线
与抛物线 只有一个公共点的直线有( )
只有一个公共点的直线有( ) B 2条 C 3条 D 无数多条
B 2条 C 3条 D 无数多条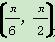 是减函数,则a的取值范围是________.
是减函数,则a的取值范围是________.