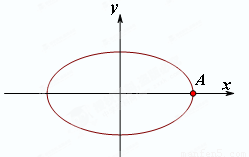
题目内容
已知圆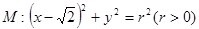 ,若椭圆
,若椭圆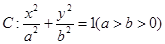 的右顶点为圆
的右顶点为圆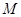 的圆心,离心率为
的圆心,离心率为 .
.
(1)求椭圆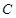 的方程;
的方程;
(2)若存在直线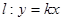 ,使得直线
,使得直线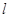 与椭圆
与椭圆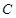 分别交于
分别交于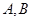 两点,与圆
两点,与圆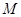 分别交于
分别交于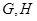 两点,点
两点,点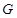 在线段
在线段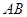 上,且
上,且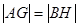 ,求圆
,求圆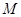 的半径
的半径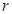 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)圆的圆心已知,可求出椭圆方程中的 ,又椭圆离心率知道根据
,又椭圆离心率知道根据  可得
可得 ,故可求出椭圆方程;(2)设出
,故可求出椭圆方程;(2)设出 两点坐标,联立椭圆方程,用弦长公式将
两点坐标,联立椭圆方程,用弦长公式将 表示成
表示成 的函数,再将
的函数,再将 表示成
表示成 的函数,根据
的函数,根据 和基本不等式求解.
和基本不等式求解.
试题解析:(1)设椭圆的焦距为2c,因为
所以椭圆的方程为 。
。
(2)设 ,
,
联立方程得
所以
则
又点 到直线
到直线 的距离
的距离 ,则
,则
显然,若点 也在线段
也在线段 上,则由对称性可知,直线
上,则由对称性可知,直线 就是y轴,与已知矛盾,所以要使
就是y轴,与已知矛盾,所以要使 ,只要
,只要 ,所以
,所以

当 时,
时, .
.
当 时,
时, 3,
3,
又显然 ,所以
,所以 。
。
综上,圆 的半径
的半径 的取值范围是
的取值范围是 .
.
考点:椭圆和直线综合、点到直线的距离公式、弦长公式、基本不等式.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
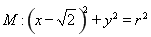
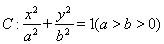

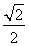
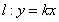
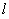
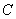
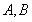
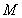
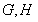


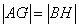
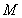

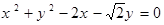 经过椭圆
经过椭圆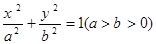 的右焦点F及上顶点B.过椭圆外一点
的右焦点F及上顶点B.过椭圆外一点
 且倾斜角为
且倾斜角为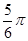 的直线
的直线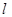 交椭圆于C、D两点.
交椭圆于C、D两点.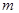 的取值范围。
的取值范围。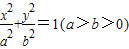 的右顶点,若点
的右顶点,若点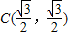 在椭圆上,且满足
在椭圆上,且满足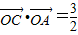 .(其中O为坐标原点)
.(其中O为坐标原点)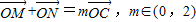 时,求△OMN面积的最大值.
时,求△OMN面积的最大值.
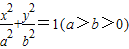 的右顶点,若点
的右顶点,若点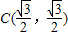 在椭圆上,且满足
在椭圆上,且满足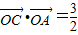 .(其中O为坐标原点)
.(其中O为坐标原点)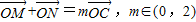 时,求△OMN面积的最大值.
时,求△OMN面积的最大值.