题目内容

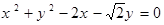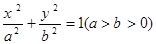已知圆G:经过椭圆的右焦点F及上顶点B.过椭圆外一点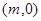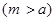且倾斜角为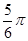的直线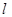交椭圆于C、D两点.

(1) 求椭圆方程；

(2) 若右焦点F在以CD为直径的圆E的内部，求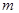的取值范围。

 

【答案】

（1）（2） ＜m＜．

【解析】本试题主要是考查了椭圆方程的求解，以及直线与椭圆的位置关系的综合运用。联立方程组结合判别式得到参数的范围。

（1）依据题意可求得F，B的坐标，求得c和b，进而求得a，则椭圆的方程可得

2）设出直线l的方程，与椭圆方程联立消去，利用判别式大于0求得m的范围，设出C，D的坐标，利用韦达定理表示出x1+x2和进而利用直线方程求得y1y2，表示出FC

和 FD ，进而求得 FC • FD 的表达式，利用F在圆E的内部判断出 FC • FD ＜0求得m的范围，最后综合可求得m范围

 

练习册系列答案
相关题目
如图，已知圆G：x2+y2-2x-
2
y=0经过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F及上顶点B，过椭圆外一点（m，0）（ma）且倾斜角为
5
6
π的直线l交椭圆于C，D两点．
（Ⅰ）求椭圆的方程；
（Ⅱ）若
FC
•
FD
＜0，求m的取值范围．
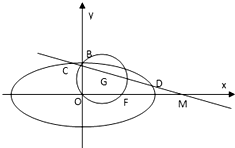如图，已知圆G：x2+y2-2x-
2
y=0经过椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F及上顶点B．过点M（m，0）作倾斜角为
5
6
π的直线l交椭圆于C、D两点．
（1）求椭圆的方程；
（2）若点Q（1，0）恰在以线段CD为直径的圆的内部，求实数m范围．
（2012•虹口区三模）已知圆G：x2+y2-2x-
2
y=0经过椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F及上顶点B．
（1）求椭圆的方程；
（2）过椭圆外一点M（m，0）（m＞a）倾斜角为
5
6
π的直线l交椭圆于C、D两点，若右焦点F在以线段CD为直径的圆E的外部，求m的取值范围．
已知圆G：x2+y2-2
2
x-2y=0经过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F及上顶点B．
（1）求椭圆的方程；
（2）过椭圆外一点M（m，0）（m＞a）倾斜角为
2
3
π的直线l交椭圆于C、D两点，若点N（3，0）在以线段CD为直径的圆E的外部，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网