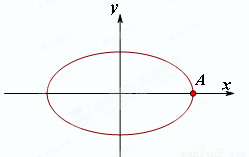
题目内容
如图,已知点A是椭圆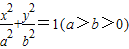 的右顶点,若点
的右顶点,若点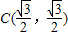 在椭圆上,且满足
在椭圆上,且满足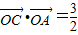 .(其中O为坐标原点)
.(其中O为坐标原点)(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与椭圆交于两点M,N,当
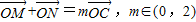 时,求△OMN面积的最大值.
时,求△OMN面积的最大值.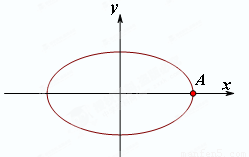
【答案】分析:(Ⅰ)由点 在椭圆
在椭圆 上,知
上,知 ,由
,由 ,知
,知 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
(Ⅱ)设M(x1,y1),N(x2,y2),由 ,知
,知 ,利用点差法得到直线
,利用点差法得到直线 ,由此能求出△OMN面积的最大值.
,由此能求出△OMN面积的最大值.
解答:解:(Ⅰ)∵点 在椭圆
在椭圆 上,
上,
∴ ,
,
∵ ,
,
∴ ,解得a=3,∴b=1.
,解得a=3,∴b=1.
∴椭圆的方程为 =1.
=1.
(Ⅱ)设M(x1,y1),N(x2,y2),
∵ ,
,
∴ ,
,
设直线 ,
,
由 ,得:4y2-6ny+3n2-1=0
,得:4y2-6ny+3n2-1=0
则 ,
,
∴ ,
,
点O到直线l的距离d= ,
,
∴S=
=
≤ =
= .
.
当且仅当3n2=4-3n2,n=± .
.
∵m∈(0,2),∴m= .
.
∴当m= 时,△OMN面积的最大值为
时,△OMN面积的最大值为 .
.
点评:本题考查椭圆方程的求法,考查三角形面积的最大值的求法.解题时要认真审题,仔细解答,注意点差法和等价转化思想的合理运用.
 在椭圆
在椭圆 上,知
上,知 ,由
,由 ,知
,知 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.(Ⅱ)设M(x1,y1),N(x2,y2),由
 ,知
,知 ,利用点差法得到直线
,利用点差法得到直线 ,由此能求出△OMN面积的最大值.
,由此能求出△OMN面积的最大值.解答:解:(Ⅰ)∵点
 在椭圆
在椭圆 上,
上,∴
 ,
,∵
 ,
,∴
 ,解得a=3,∴b=1.
,解得a=3,∴b=1.∴椭圆的方程为
 =1.
=1.(Ⅱ)设M(x1,y1),N(x2,y2),
∵
 ,
,∴
 ,
,
设直线
 ,
,由
 ,得:4y2-6ny+3n2-1=0
,得:4y2-6ny+3n2-1=0则
 ,
,∴
 ,
,点O到直线l的距离d=
 ,
,∴S=

=

≤
 =
= .
.当且仅当3n2=4-3n2,n=±
 .
.∵m∈(0,2),∴m=
 .
.∴当m=
 时,△OMN面积的最大值为
时,△OMN面积的最大值为 .
.点评:本题考查椭圆方程的求法,考查三角形面积的最大值的求法.解题时要认真审题,仔细解答,注意点差法和等价转化思想的合理运用.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 如图,已知点A是椭圆
如图,已知点A是椭圆 如图,已知点B是椭圆
如图,已知点B是椭圆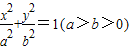 的右顶点,若点
的右顶点,若点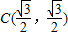 在椭圆上,且满足
在椭圆上,且满足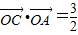 .(其中O为坐标原点)
.(其中O为坐标原点)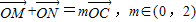 时,求△OMN面积的最大值.
时,求△OMN面积的最大值.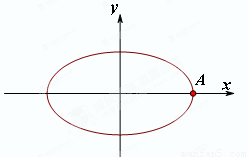
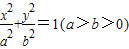 的右顶点,若点
的右顶点,若点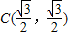 在椭圆上,且满足
在椭圆上,且满足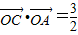 .(其中O为坐标原点)
.(其中O为坐标原点)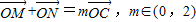 时,求△OMN面积的最大值.
时,求△OMN面积的最大值.