题目内容
已知圆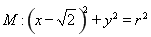
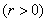 ,若椭圆
,若椭圆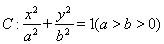 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为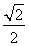 .
.
(1)求椭圆C的方程;
(2)若存在直线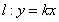 ,使得直线
,使得直线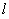 与椭圆
与椭圆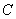 分别交于
分别交于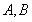 两点,与圆
两点,与圆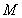 分别交于
分别交于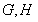 两点,点
两点,点 在线段
在线段 上,且
上,且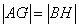 ,求圆
,求圆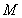 的半径
的半径 的取值范围.
的取值范围.
【答案】
(1)  (2)
(2) 
【解析】
试题分析:,
(1)从圆的标准方程得到圆心的坐标即为椭圆的右顶点,即可得到a值,再由椭圆离心率、a值结合、abc之间的关系可得到b值,即得到椭圆的标准方程
(2)联立直线与椭圆方程并利用弦长公式可用斜率k表示弦长|AB|,|GH|.由对称性得到|AB|=|GH|,得到r关于k的表达式,再根据表达式可以利用函数值域求法中的换元法解得r的取值范围.
试题解析:
(1)设椭圆的焦距为2C,因为a= ,
, ,
, ,所以椭圆C的方程为
,所以椭圆C的方程为 .
.
(2)设A ,联立直线与椭圆方程得
,联立直线与椭圆方程得

 ,则
,则 ,又因为点M(
,又因为点M( )到直线l的距离d=
)到直线l的距离d= 。所以
。所以 ,显然若点H也在直线AB上,则由对称性可知,直线y=kx就是y轴与已知矛盾,所以要使得|AG|=|BH|,只要|AB|=|GH|,所以
,显然若点H也在直线AB上,则由对称性可知,直线y=kx就是y轴与已知矛盾,所以要使得|AG|=|BH|,只要|AB|=|GH|,所以
 ,
,
当k=0时, ,当k
,当k 时,
时,  ,由于
,由于


 ,综上
,综上 .
.
考点:椭圆方程极其性质 弦长

练习册系列答案
相关题目
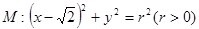 ,若椭圆
,若椭圆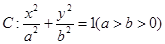 的右顶点为圆
的右顶点为圆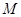 的圆心,离心率为
的圆心,离心率为 .
.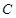 的方程;
的方程;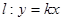 ,使得直线
,使得直线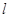 与椭圆
与椭圆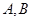 两点,与圆
两点,与圆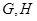 两点,点
两点,点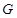 在线段
在线段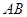 上,且
上,且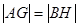 ,求圆
,求圆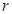 的取值范围.
的取值范围. 经过椭圆
经过椭圆 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点 作倾斜角为
作倾斜角为 的直线
的直线 交椭圆于C、D两点.
交椭圆于C、D两点.
 恰在以线段CD为直径
恰在以线段CD为直径 范围.
范围.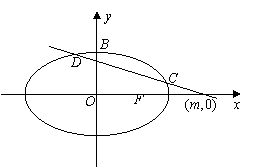 (2)若
(2)若 如图6,已知圆
如图6,已知圆