已知A.B.C三点不共线.O为平面ABC外的一点.$\overrightarrow{OP}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{7}{3}$$\overrightarrow{OB}$+$λ\overrightarrow{OC}$确定的点P与A.B.C四点共面.则λ的值为-$\frac{23}{15}$．题目和参考答案——青夏教育精英家教网——

题目内容

18．已知A、B、C三点不共线，O为平面ABC外的一点，$\overrightarrow{OP}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{7}{3}$$\overrightarrow{OB}$+$λ\overrightarrow{OC}$（λ∈R）确定的点P与A、B、C四点共面，则λ的值为-$\frac{23}{15}$．

分析利用向量共面定理即可得出．

解答解：∵点P与A、B、C四点共面，$\overrightarrow{OP}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{7}{3}$$\overrightarrow{OB}$+$λ\overrightarrow{OC}$，
∴$\frac{1}{5}$$+\frac{7}{3}$+λ=1，解得λ=-$\frac{23}{15}$．
故答案为-$\frac{23}{15}$．

点评本题考查了向量共面定理，属于基础题．

练习册系列答案

名师点金紧贴课标同步训练系列答案

1加1单元夺金系列答案

标准期末考卷系列答案

全优课堂同步精讲巧拨系列答案

好帮手全程测控系列答案

名师点睛满分试卷系列答案

上教社导学案系列答案

初中优选测试卷系列答案

高效课堂宝典训练系列答案

畅响双优卷系列答案

相关题目

8．已知实数m＞0，函数f（x）=$\frac{2{x}^{2}-sinx+2}{{x}^{2}+1}$在[-m，m]上的最大值为p，最小值为q，则p+q=4．

9．设动直线l垂直于x轴，且与椭圆x²+2y²=4交于A，B两点，P是l上满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=-1的点．
（1）求动点P的轨迹方程；
（2）设点C（-2，0），若过点C的直线与动点P的轨迹恰有一个公共点，求该直线的斜率．

6．已知F₁（-2，0），F₂（2，0）直线l：x+y-4=0，点P在直线l上，则过点P以F₁，F₂为焦点且长轴最短的椭圆标准方程为$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1．

13．已知函数f（x）=2cos（x-$\frac{2}{3}$π）+2cosx，x∈[$\frac{π}{2}$，π]．
（1）若sinx=$\frac{4}{5}$，求函数f（x）的值；
（2）求函数f（x）的值域．

3．设a、b∈R，且a、b不同时为零，则（$\frac{a+bi}{b-ai}$）¹⁵=-i．

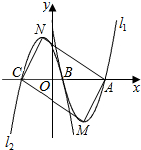如图，己知抛物线1₁：y=x²-8x+12与x轴分别交于A、B两点，顶点为M．将抛物线1₁关于x轴作轴对称变换后再向左平移得到抛物线1₂，若抛物线1₂过点B，与x轴的另一个交点为C，顶点为N，则四边形AMCN的面积为32．

7．已知f（x）=sinx+cosx+|sinx-cosx|，则f（x）的最小正周期为（　　）

8．已知圆的方程是x²+y²=4，求经过圆上一点M（$\sqrt{2}$，$\sqrt{2}$）的切线方程．