题目内容
在△ABC中,点B(0,1),直线AD:2x﹣y﹣4=0是角A的平分线.直线CE:x﹣2y﹣6=0是AB边的中线.
(1)求边AC的直线方程;
(2)圆M:x2+(y+1)2=r2(1≤r≤3),自点C向圆M引切线CF,CG,切点为F、G.求: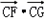 的取值范围.
的取值范围.
(1)求边AC的直线方程;
(2)圆M:x2+(y+1)2=r2(1≤r≤3),自点C向圆M引切线CF,CG,切点为F、G.求:
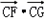 的取值范围.
的取值范围.解:(1)设AB中点坐标为(x0,y0),
∵点B(0,1),则A点坐标为(2x0,2y0﹣1).
依题意得 ,
,
解之得: ,
,
∴A(﹣2,﹣8),
由于B点关于2x﹣y﹣4=0的对称点(4,﹣1)在直线AC上.
∴直线AC的方程为 ,即 7x﹣6y﹣34=0.
,即 7x﹣6y﹣34=0.
(2)由 解得
解得 ,
,
即C(4,﹣1),
又 圆心M(0,﹣1),
∴ =
= =(16﹣r2)cos2∠CFM=(16﹣r2)(1﹣2sin2∠GCM)=
=(16﹣r2)cos2∠CFM=(16﹣r2)(1﹣2sin2∠GCM)= ,
,
∵1≤r≤3,∴1≤r2≤9,
由单调性得 =
= ,
,
 =
= .
.
∴ 的取值范围为
的取值范围为 .
.
∵点B(0,1),则A点坐标为(2x0,2y0﹣1).
依题意得
 ,
,解之得:
 ,
,∴A(﹣2,﹣8),
由于B点关于2x﹣y﹣4=0的对称点(4,﹣1)在直线AC上.
∴直线AC的方程为
 ,即 7x﹣6y﹣34=0.
,即 7x﹣6y﹣34=0.(2)由
 解得
解得 ,
,即C(4,﹣1),
又 圆心M(0,﹣1),
∴
 =
= =(16﹣r2)cos2∠CFM=(16﹣r2)(1﹣2sin2∠GCM)=
=(16﹣r2)cos2∠CFM=(16﹣r2)(1﹣2sin2∠GCM)= ,
,∵1≤r≤3,∴1≤r2≤9,
由单调性得
 =
= ,
, =
= .
.∴
 的取值范围为
的取值范围为 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的取值范围.
的取值范围.