题目内容
在△ABC中,点B(0,1),直线AD:2x-y-4=0是角A的平分线.直线CE:x-2y-6=0是AB边的中线.
(1)求边AC的直线方程;
(2)圆M:x2+(y+1)2=r2(1≤r≤3),自点C向圆M引切线CF,CG,切点为F、G.求:
•
的取值范围.
(1)求边AC的直线方程;
(2)圆M:x2+(y+1)2=r2(1≤r≤3),自点C向圆M引切线CF,CG,切点为F、G.求:
| CF |
| CG |
分析:(1)设AB中点坐标为D(x0,y0),∵点B(0,1),则A点坐标为(2x0,2y0-1),把D(x0,y0)代入直线CE方程,把A点坐标(2x0,2y0-1)代入角A的平分线方程,求出x0,y0
的值,可得A点坐标.再由B点关于2x-y-4=0的对称点(4,-1)在直线AC上,由两点式求直线AC的方程.
(2)把CE和AC的方程联立方程组求出点C的坐标,利用两个向量的数量积的定义求出
•
=
[(r2-12)2-16],再由二次函数的性质求得
•
的最大值和最小值,
从而得到
•
的取值范围.
的值,可得A点坐标.再由B点关于2x-y-4=0的对称点(4,-1)在直线AC上,由两点式求直线AC的方程.
(2)把CE和AC的方程联立方程组求出点C的坐标,利用两个向量的数量积的定义求出
| CG |
| CF |
| 1 |
| 8 |
| CF |
| CG |
从而得到
| CF |
| CG |
解答:解:(1)设AB中点坐标为(x0,y0),∵点B(0,1),则A点坐标为(2x0,2y0-1).
依题意得
,解之得:
,∴A(-2,-8),
由于B点关于2x-y-4=0的对称点(4,-1)在直线AC上.∴直线AC的方程为
=
,即 7x-6y-34=0.
(2)由
解得
,即C(4,-1),又 圆心M(0,-1),
∴
•
=|
|•|
|•cos∠FCG=(16-r2)cos2∠CFM=(16-r2)(1-2sin2∠GCM)=(16-r2)[1-2(
)2]=
[(r2-12)2-16],
∵1≤r≤3,∴1≤r2≤9,由单调性得
•
|max=
×(121-16)=
,
•
|min=
×(9-16)=-
.
∴
•
的取值范围为[-
,
].
依题意得
|
|
由于B点关于2x-y-4=0的对称点(4,-1)在直线AC上.∴直线AC的方程为
| y+1 |
| -8+1 |
| x-4 |
| -2-4 |
(2)由
|
|
∴
| CG |
| CF |
| CG |
| CF |
| r |
| 4 |
| 1 |
| 8 |
∵1≤r≤3,∴1≤r2≤9,由单调性得
| CG |
| CF |
| 1 |
| 8 |
| 105 |
| 8 |
| CG |
| CF |
| 1 |
| 8 |
| 7 |
| 8 |
∴
| CG |
| CF |
| 7 |
| 8 |
| 105 |
| 8 |
点评:本题主要考查两个向量的数量积的定义,用两点式求直线方程,圆的切线性质,以及在闭区间上求二次函数的最值,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
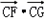 的取值范围.
的取值范围. 的取值范围.
的取值范围.