题目内容
在△ABC中,点B(-6,0)、C(0,8),且sinB、sinA、sinC成等差数列.
(1)求证:顶点A在一个椭圆上运动.
(2)指出这个椭圆的焦点坐标以及焦距.
答案:
解析:
提示:
解析:
|
解:(1)证明:由题意得sinB+sinC=2sinA,由正弦定理,得sinB= (2)这个椭圆的焦点坐标分别是(-6,0)、(0,8),焦距是10. 解析:本题依据等差数列的定义以及结合正弦定理将已知转化为相应的边间的关系,再利用椭圆的定义将问题解决. |
提示:
|
有关证明或判定动点的轨迹是椭圆这样的问题,可以紧紧围绕着相应的椭圆的定义,去探寻相应的动点到某两个定点的距离的和等于一个常数,并且注意这个常数与这两个定点之间的距离的大小关系,从而确定. |

练习册系列答案
相关题目
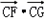 的取值范围.
的取值范围. 的取值范围.
的取值范围.