Question

【题目】在平面直角坐标系中，已知直线的方程为，.

（1）若直线在轴、轴上的截距之和为-1，求坐标原点到直线的距离；

（2）若直线与直线：和：分别相交于、两点，点到、两点的距离相等，求的值.

Answer 1

【答案】（1）（2）

【解析】

(1)根据直线在轴、轴上的截距之和为-1,列等式可得,从而可得直线的方程,再用点到直线的距离公式可得答案;

(2)先判断得点为线段的中点,设出,根据中点公式求出,将其代入直线可解得的坐标,再将的坐标代入的方程可解得.

（1）解法一：令得横截距；

令，得横截距；

则有，解得，

此时，直线的方程为，即.

坐标原点到直线的距离.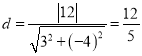

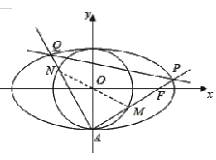
（2）∵点在直线上，且点到、距离相等，

∴点为线段的中点，

如图所示:

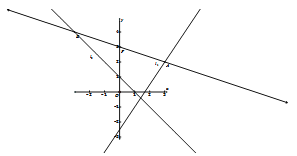
设直线与：的交点为，则直线与：的交点.

∴，

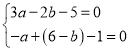解得.

∴.

又∵点在直线上，

∴，

解得.