题目内容
已知双曲线C:(1)求双曲线C的方程;
(2)设t=![]() ·
·![]() +
+![]() ·
·![]() (O为坐标原点),求t的取值范围.
(O为坐标原点),求t的取值范围.
解:(1)由e=![]() =2,
=2,
∴c=2a.
∴b2=c2-a2=3a2,即b=![]() a.
a.
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() .
.
∴双曲线C的右准线方程为x=![]() ,渐近线方程为y=±
,渐近线方程为y=±![]() x.
x.
由 解得
解得
故一条准线与两条渐近线所围成的三角形的面积为S=2×![]() ×
×![]() ×
×![]() =
=![]() .
.
可得a2=4,b2=3a2=12,
故所求双曲线C的方程为![]() -
-![]() =1.
=1.
(2)由条件知直线斜率一定存在,设其为k,则直线l的方程为y=kx-2,
代入![]() -
-![]() =1,可得(3-k2)x2+4kx-16=0.
=1,可得(3-k2)x2+4kx-16=0.
∵直线l与双曲线C交于相异两点,
∴
解得k2<4且k2≠3,
设M(x1,y1),N(x2,y2),则
∴t=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() ·(
·(![]() +
+![]() )
)
=![]() ·
·![]() =x1x2+y1y2=x1x2+(kx1-2)(kx2-2)
=x1x2+y1y2=x1x2+(kx1-2)(kx2-2)
=(k2+1)x1x2-2k(x1+x2)+4
=![]() =
=![]() ,
,
又0≤k2<4且k2≠3,
∴![]() ∈(-∞,-
∈(-∞,-![]() ]∪(1,+∞).
]∪(1,+∞).
∴t的取值范围为(-∞,-![]() ]∪(52,+∞).
]∪(52,+∞).

练习册系列答案
相关题目








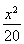




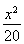

 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 焦点到渐近线的距离为
焦点到渐近线的距离为

 与C有两个不同的交点,求实数k的取值范围;
与C有两个不同的交点,求实数k的取值范围; 求实数k的值.
求实数k的值.