题目内容
椭圆C1的中心在原点,过点(0,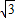 ),且右焦点F2与圆C2:(x-1)2+y2=
),且右焦点F2与圆C2:(x-1)2+y2= 的圆心重合.
的圆心重合.(1)求椭圆C1的方程;
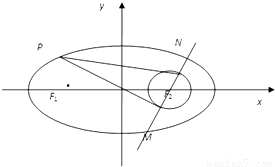
(2)过点F2的直线l交椭圆于M、N两点,问是否存在这样的直线l,使得以MN为直径的圆过椭圆的左焦点F1?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(1)利用椭圆和圆的标准方程及其性质即可得出;
(2)以MN为直径的圆过F1?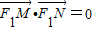 .分类讨论直线l的斜率,当斜率存在时,把直线l的方程与椭圆的方程联立得到根与系数的关系,利用向量的数量积运算即可得出.
.分类讨论直线l的斜率,当斜率存在时,把直线l的方程与椭圆的方程联立得到根与系数的关系,利用向量的数量积运算即可得出.
解答:解:(1)依题意得F2(1,0),∴c=1,又过点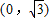 ,∴b=
,∴b=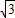 .
.
因此a2=b2+c2=4.
故所求的椭圆C1 的方程为: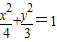 .
.
(2)由(1)知F1(-1,0).以MN为直径的圆过F1?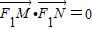 .
.
①若直线l的斜率不存在.易知N (1, ),M (1,-
),M (1,- ).
).
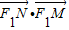 =
=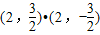 =
=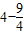 ≠0,不合题意,应舍去.
≠0,不合题意,应舍去.
②若直线l的斜率k存在,可设直线为y=k(x-1),M(x1,y1),N(x2,y2).
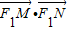 =(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2
=(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2
=x1x2+x1+x2+k(x1-1)•k(x2-1)
=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2(*)
联立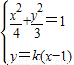 消去y得:(3+4k2)x2-8k2x+4k2-12=0.
消去y得:(3+4k2)x2-8k2x+4k2-12=0.
∴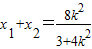 ,
,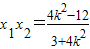 代入(*).
代入(*).
得: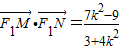 .
.
由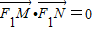 得:
得: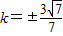 .
.
点评:熟练掌握椭圆和圆的标准方程及其性质、MN为直径的圆过F1?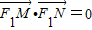 、分类讨论思想方法、直线与椭圆相交问题转化为把直线l的方程与椭圆的方程联立得到根与系数的关系、向量的数量积运算等是解题的关键.
、分类讨论思想方法、直线与椭圆相交问题转化为把直线l的方程与椭圆的方程联立得到根与系数的关系、向量的数量积运算等是解题的关键.
(2)以MN为直径的圆过F1?
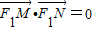 .分类讨论直线l的斜率,当斜率存在时,把直线l的方程与椭圆的方程联立得到根与系数的关系,利用向量的数量积运算即可得出.
.分类讨论直线l的斜率,当斜率存在时,把直线l的方程与椭圆的方程联立得到根与系数的关系,利用向量的数量积运算即可得出.解答:解:(1)依题意得F2(1,0),∴c=1,又过点
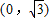 ,∴b=
,∴b=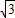 .
.因此a2=b2+c2=4.
故所求的椭圆C1 的方程为:
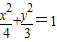 .
.(2)由(1)知F1(-1,0).以MN为直径的圆过F1?
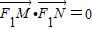 .
.①若直线l的斜率不存在.易知N (1,
 ),M (1,-
),M (1,- ).
).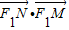 =
=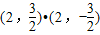 =
=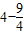 ≠0,不合题意,应舍去.
≠0,不合题意,应舍去.②若直线l的斜率k存在,可设直线为y=k(x-1),M(x1,y1),N(x2,y2).
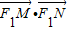 =(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2
=(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2=x1x2+x1+x2+k(x1-1)•k(x2-1)
=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2(*)
联立
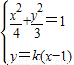 消去y得:(3+4k2)x2-8k2x+4k2-12=0.
消去y得:(3+4k2)x2-8k2x+4k2-12=0.∴
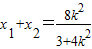 ,
,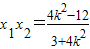 代入(*).
代入(*).得:
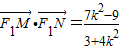 .
.由
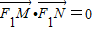 得:
得: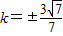 .
.点评:熟练掌握椭圆和圆的标准方程及其性质、MN为直径的圆过F1?
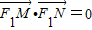 、分类讨论思想方法、直线与椭圆相交问题转化为把直线l的方程与椭圆的方程联立得到根与系数的关系、向量的数量积运算等是解题的关键.
、分类讨论思想方法、直线与椭圆相交问题转化为把直线l的方程与椭圆的方程联立得到根与系数的关系、向量的数量积运算等是解题的关键. 
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
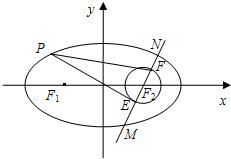 椭圆C1的中心在原点,过点(0,
椭圆C1的中心在原点,过点(0, (2005•海淀区二模)设椭圆C1的中心在原点,其右焦点与抛物线C2:y2=4x的焦点F重合,过点F与x轴垂直的直线与C1交于A、B两点,与C2交于C、D两点,已知
(2005•海淀区二模)设椭圆C1的中心在原点,其右焦点与抛物线C2:y2=4x的焦点F重合,过点F与x轴垂直的直线与C1交于A、B两点,与C2交于C、D两点,已知