题目内容
已知:向量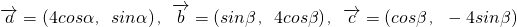
(1)若tanαtanβ=16,求证: ;
;
(2)若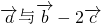 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;
(3)求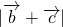 的最大值.
的最大值.
解:(1)∵tanαtanβ=16,∴sinαsinβ=16cosαcosβ,
∵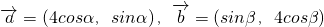 ,
,
∴4cosα•4cosβ=sinα•sinβ,
∴ ;
;
(2)∵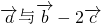 垂直,∴
垂直,∴ ,
,
即4cosαsinβ+4sinαcosβ-2(4cosαcosβ-4sinαsinβ)=0,
∴4sin(α+β)-8cos(α+β)=0,
∴tan(α+β)=2;
(3) =(sinβ+cosβ,4cosβ-4sinβ),
=(sinβ+cosβ,4cosβ-4sinβ),
∴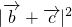 =(sinβ+cosβ)2+(4cosβ-4sinβ)2
=(sinβ+cosβ)2+(4cosβ-4sinβ)2
=17-30sinβcosβ=17-15sin2β
∴当sin2β=-1时,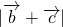 取最大值
取最大值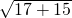 =
=
分析:(1)由题意可得sinαsinβ=16cosαcosβ,即4cosα•4cosβ=sinα•sinβ,进而可得平行;
(2)由垂直可得数量积为0,展开后由三角函数的公式可得tan(α+β)的值;
(3)可得 的坐标,进而可得模长平方的不等式,由三角函数的知识可得最值,开方可得.
的坐标,进而可得模长平方的不等式,由三角函数的知识可得最值,开方可得.
点评:本题考查向量的平行和垂直,以及三角函数的综合应用,属基础题.
∵
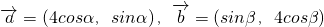 ,
,∴4cosα•4cosβ=sinα•sinβ,
∴
 ;
;(2)∵
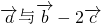 垂直,∴
垂直,∴ ,
,即4cosαsinβ+4sinαcosβ-2(4cosαcosβ-4sinαsinβ)=0,
∴4sin(α+β)-8cos(α+β)=0,
∴tan(α+β)=2;
(3)
 =(sinβ+cosβ,4cosβ-4sinβ),
=(sinβ+cosβ,4cosβ-4sinβ),∴
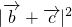 =(sinβ+cosβ)2+(4cosβ-4sinβ)2
=(sinβ+cosβ)2+(4cosβ-4sinβ)2=17-30sinβcosβ=17-15sin2β
∴当sin2β=-1时,
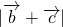 取最大值
取最大值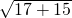 =
=
分析:(1)由题意可得sinαsinβ=16cosαcosβ,即4cosα•4cosβ=sinα•sinβ,进而可得平行;
(2)由垂直可得数量积为0,展开后由三角函数的公式可得tan(α+β)的值;
(3)可得
 的坐标,进而可得模长平方的不等式,由三角函数的知识可得最值,开方可得.
的坐标,进而可得模长平方的不等式,由三角函数的知识可得最值,开方可得.点评:本题考查向量的平行和垂直,以及三角函数的综合应用,属基础题.

练习册系列答案
相关题目
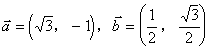 (1)证明:
(1)证明:
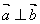 ;
;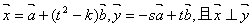 ,试求
,试求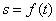 的函数关系式;
的函数关系式; 上是增函数,试求k的取值范围。
上是增函数,试求k的取值范围。