题目内容
已知平面向量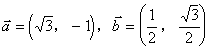
（1）证明：
；（2）若存在不同时为零的实数k和t，使
，且
，试求函数关系式
；（3）根据（2）的结论，讨论关于t的方程
的解的情况。
解：①
②
，即
整理得：
因为：
，则
③
且方程
的解的情况可以看作曲线
与直线
的交点的个数
时，与
有两个交点，因此方程有两解；
时，与有一个交点，因此方程有一解；
时，与没有交点，因此方程无解。
练习册系列答案
名校课堂系列答案
相关题目
已知平面向量
=(1，-m)，
=(m2 ， m)，则向量
+
（ ）
| a |
| b |
| a |
| b |
| A、平行于x轴 |
| B、平行于第一、三象限的角平分线 |
| C、平行于y轴 |
| D、平行于第二、四象限的角平分线 |
已知平面向量
=(1，1)，
=(1，-1)，则向量
-
=（ ）
| a |
| b |
| 1 |
| 2 |
| a |
| 3 |
| 2 |
| b |
| A、（-2，-1） |
| B、（-1，2） |
| C、（-1，0） |
| D、（-2，1） |