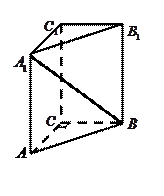题目内容
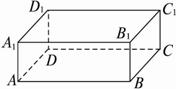
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.
(1)求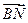 的长;
的长;
(2)求cos<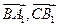 >的值;
>的值;
(3)求证: A1B⊥C1M.

(1)求
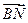 的长;
的长;(2)求cos<
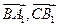 >的值;
>的值;(3)求证: A1B⊥C1M.
(1)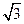 (2)
(2)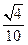 (3)证明略
(3)证明略
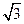 (2)
(2)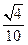 (3)证明略
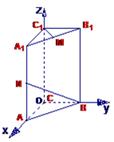
(3)证明略 如图,以C为原点建立空间直角坐标系O-xyz.
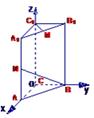
依题意得: B(0,1,0),N(1,0,1)
∴|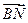 |=
|=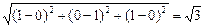 .
.
(2)解: 依题意得 A1(1,0,2),C(0,0,0),B1(0,1,2).
A1(1,0,2),C(0,0,0),B1(0,1,2).
∴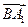 =
=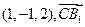 =(0,1,2)
=(0,1,2)
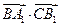 =1×0+(-1)×1+2×2=3
=1×0+(-1)×1+2×2=3
|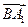 |=
|=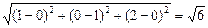
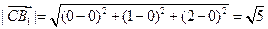
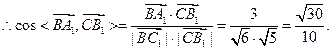
(3)证明:依题意得 C1(0,0,2),M(
C1(0,0,2),M(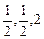 )
)
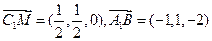
∴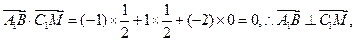
∴A1B⊥C1M.

依题意得: B(0,1,0),N(1,0,1)
∴|
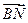 |=
|=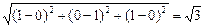 .
.(2)解: 依题意得
 A1(1,0,2),C(0,0,0),B1(0,1,2).
A1(1,0,2),C(0,0,0),B1(0,1,2).∴
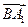 =
=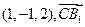 =(0,1,2)
=(0,1,2)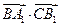 =1×0+(-1)×1+2×2=3
=1×0+(-1)×1+2×2=3|
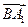 |=
|=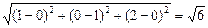
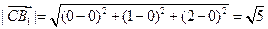
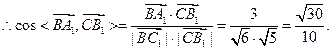
(3)证明:依题意得
 C1(0,0,2),M(
C1(0,0,2),M(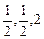 )
)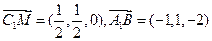
∴
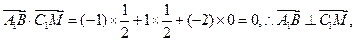
∴A1B⊥C1M.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 是圆内接四边形.
是圆内接四边形.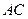 与
与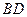 的交点为
的交点为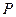 ,
,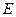 是弧
是弧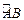 上一点,连接
上一点,连接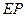 并延长交
并延长交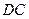 于点
于点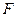 ,点
,点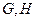 分别在
分别在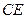 ,
,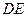 的延长线上,满足
的延长线上,满足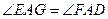 ,
,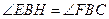 ,求证:
,求证: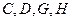 四点共圆.
四点共圆. 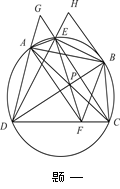
 -ABCD中,侧面PAD为正三角形,底面为正方
-ABCD中,侧面PAD为正三角形,底面为正方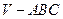 中,
中,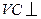 底面
底面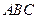 ,
,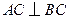 ,
,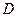 是
是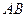 的中点,且
的中点,且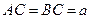 ,
,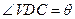
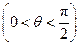 .
.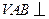 平面
平面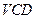 ;(2)当角
;(2)当角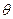 变化时,求直线
变化时,求直线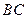 与平面
与平面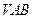 所成的角
所成的角 直三棱柱
直三棱柱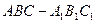 中,
中,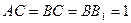 ,
,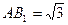 .
.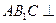 平面
平面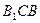 ;
;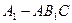 的体积.
的体积.
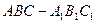 中,
中,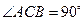 ,
,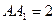 ,
,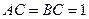 ,则异面直线
,则异面直线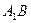 与
与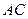 所成角的
所成角的