题目内容
 直三棱柱
直三棱柱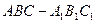 中,
中,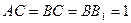 ,
,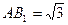 .
.(1)求证:平面
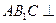 平面
平面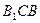 ;
;(2)求三棱锥
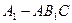 的体积.
的体积.
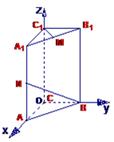
解:(1)直三棱柱ABC—A1B1C1中,BB1⊥底面ABC,
则BB1⊥AB,BB1⊥BC,
又由于AC=BC=BB1=1,AB1= ,则AB=
,则AB= ,
,
则由AC2+BC2=AB2可知,AC⊥BC,
又由上BB1⊥底面ABC可知BB1⊥AC,则AC⊥平面B1CB,
所以有平面AB1C⊥平面B1CB;-
(2)三棱锥A1—AB1C的体积 .
.
则BB1⊥AB,BB1⊥BC,
又由于AC=BC=BB1=1,AB1=
 ,则AB=
,则AB= ,
,则由AC2+BC2=AB2可知,AC⊥BC,
又由上BB1⊥底面ABC可知BB1⊥AC,则AC⊥平面B1CB,
所以有平面AB1C⊥平面B1CB;-
(2)三棱锥A1—AB1C的体积
 .
.
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 ,BC=
,BC= ,则P-ABC的体积V的取值范围是_____________。
,则P-ABC的体积V的取值范围是_____________。
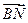 的长;
的长;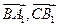 >的值;
>的值; ,棱长为
,棱长为 的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个平面上,则此球的体积为 . 如图,在三棱锥P-ABC中, PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1.
如图,在三棱锥P-ABC中, PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1.