题目内容
如题一图,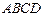 是圆内接四边形.
是圆内接四边形.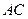 与
与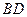 的交点为
的交点为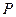 ,
,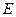 是弧
是弧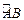 上一点,连接
上一点,连接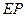 并延长交
并延长交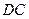 于点
于点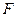 ,点
,点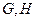 分别在
分别在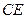 ,
,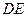 的延长线上,满足
的延长线上,满足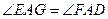 ,
,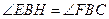 ,求证:
,求证: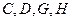 四点共圆.
四点共圆.
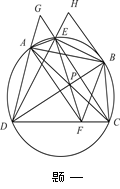
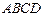 是圆内接四边形.
是圆内接四边形.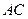 与
与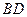 的交点为
的交点为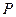 ,
,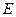 是弧
是弧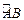 上一点,连接
上一点,连接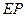 并延长交
并延长交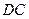 于点
于点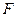 ,点
,点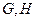 分别在
分别在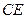 ,
,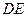 的延长线上,满足
的延长线上,满足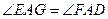 ,
,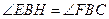 ,求证:
,求证: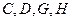 四点共圆.
四点共圆. 
[证] 由已知条件知

 .
.
又 ,
,
所以 ,
,
从而 四点共圆,此圆记为
四点共圆,此圆记为 .
.
同理可证: 四点共圆,此圆记为
四点共圆,此圆记为 .
.
点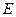 在圆
在圆 ,
, 内.延长
内.延长 与圆
与圆 相交于点
相交于点 ,则
,则
 ,
,
故 四点共圆.
四点共圆.
所以 在
在 的外接圆上,故
的外接圆上,故 在
在 上.
上.
再用相交弦定理:
 ,
,
故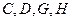 四点共圆.
四点共圆.

 .
.又
 ,
,所以
 ,
,从而
 四点共圆,此圆记为
四点共圆,此圆记为 .
.同理可证:
 四点共圆,此圆记为
四点共圆,此圆记为 .
. 点
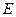 在圆
在圆 ,
, 内.延长
内.延长 与圆
与圆 相交于点
相交于点 ,则
,则 ,
,故
 四点共圆.
四点共圆. 所以
 在
在 的外接圆上,故
的外接圆上,故 在
在 上.
上. 再用相交弦定理:
 ,
,故
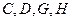 四点共圆.
四点共圆. 解析见答案

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
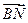 的长;
的长;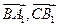 >的值;
>的值;

 ⊙O所在的平面,
⊙O所在的平面, 是⊙O的直径,
是⊙O的直径, ,
, C是⊙O上一点,且
C是⊙O上一点,且 ,
, 与⊙O所在的平面成
与⊙O所在的平面成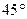 角,
角, 是
是 ;(Ⅱ) 求证:
;(Ⅱ) 求证: ;
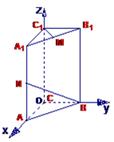
; 如图,在三棱锥P-ABC中, PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1.
如图,在三棱锥P-ABC中, PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1.
 和
和 ,
, 、
、 分别为
分别为 、
、 的中点,每两条弦的两端都在球面上运动,有下面四个命题:①弦
的中点,每两条弦的两端都在球面上运动,有下面四个命题:①弦 的最大值为5 ④
的最大值为5 ④ 是空间两条不同直线,
是空间两条不同直线, 是两个不同平面,下面有四个命题:
是两个不同平面,下面有四个命题: ②
②
 ④
④
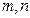 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( ) ,则
,则
 则
则
 ,则
,则
 则
则