题目内容
2.矩形ABCD的顶点A,B在直线y=2x+m上,C,D在抛物线y2=4x上,该矩形的外接圆方程为x2+y2-x-4y-t=0.(1)求矩形ABCD对角线交点M的坐标;
(2)求此矩形的长,并求m,t的值.
分析 (1)矩形ABCD对角线交点M,即矩形的外接圆圆心,由矩形的外接圆方程,可得答案;
(2)设矩形ABCD的顶点C,D的坐标为:($\frac{1}{4}{a}^{2}$,a),($\frac{1}{4}{b}^{2}$,b),矩形ABCD的顶点A,B的坐标为:(1-$\frac{1}{4}{a}^{2}$,4-a),(1-$\frac{1}{4}{b}^{2}$,4-b),则kAB=2,kBC=-$\frac{1}{2}$,可得a,b的值,进而得到m,t的值.
解答 解:(1)矩形ABCD对角线交点M,即矩形的外接圆圆心,
由矩形的外接圆方程为x2+y2-x-4y-t=0.
故M点的坐标为($\frac{1}{2}$,2);
(2)设矩形ABCD的顶点C,D的坐标为:($\frac{1}{4}{a}^{2}$,a),($\frac{1}{4}{b}^{2}$,b)
矩形ABCD的顶点A,B的坐标为:(1-$\frac{1}{4}{a}^{2}$,4-a),(1-$\frac{1}{4}{b}^{2}$,4-b),
则kAB=$\frac{(4-a)-(4-b)}{(4-\frac{1}{4}{a}^{2})-(4-\frac{1}{4}{b}^{2})}$=$\frac{4}{a+b}$=2,
故a+b=2;
kBC=$\frac{a-(4-b)}{\frac{1}{4}{a}^{2}-(1-\frac{1}{4}{b}^{2})}$=-$\frac{1}{2}$,
即a2+b2=20,
解得:$\left\{\begin{array}{l}a=4\\ b=-2\end{array}\right.$,或$\left\{\begin{array}{l}a=-2\\ b=4\end{array}\right.$,
不妨令:$\left\{\begin{array}{l}a=-2\\ b=4\end{array}\right.$,则点C,D的坐标为:(1,-2),(4,4)
A,B的坐标为:(0,6),(-3,0),
则m=6,t=12.
点评 本题考查的知识点是直线与圆的位置关系,圆的一般方程,直线垂直的条件,方程思想,难度中档.

| A. | (-1,0)∪(0,+∞) | B. | [-3,+∞) | C. | [-3,-1)∪(-1,+∞) | D. | (-1,+∞) |
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
|f(x)|-|g(x)|+h(x)=$\left\{\begin{array}{l}{-2,x<-1}\\{7x+5,-1≤x<0}\\{-4x+5,x≥0}\end{array}\right.$,h(x)的解析式为.
| A. | 2x-$\frac{3}{2}$ | B. | -2x-$\frac{3}{2}$ | C. | 2x+$\frac{3}{2}$ | D. | -2x+$\frac{3}{2}$ |
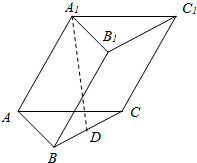 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.