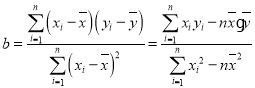题目内容
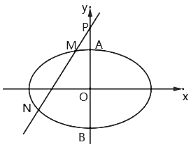
【题目】已知抛物线![]() 过点
过点![]() (
(![]() 为非零常数)与
为非零常数)与![]() 轴不垂直的直线
轴不垂直的直线![]() 与C交于
与C交于![]() 两点.
两点.
(1)求证:![]() (
(![]() 是坐标原点);
是坐标原点);
(2)AB的垂直平分线与![]() 轴交于
轴交于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设A关于![]() 轴的对称点为D,求证:直线BD过定点,并求出定点的坐标.
轴的对称点为D,求证:直线BD过定点,并求出定点的坐标.
【答案】(1)见解析;(2) ![]() ;(3) 过定点,且定点为
;(3) 过定点,且定点为![]() .
.
【解析】
(1)因为![]() ,所以联立直线和曲线方程,得到
,所以联立直线和曲线方程,得到![]() 的表达式,代入计算即可证明结果. (2)首先根据第一问的计算过程求出
的表达式,代入计算即可证明结果. (2)首先根据第一问的计算过程求出![]() 的中点坐标
的中点坐标![]() ,从而设出AB的垂直平分线:
,从而设出AB的垂直平分线:![]() ,令
,令![]() ,求出
,求出![]() 的表达式
的表达式![]() ,根据第一问中
,根据第一问中![]() 求出
求出![]() 的关系,代入求解
的关系,代入求解![]() 的范围即可. (3)首先根据对称关系设出D点的坐标,然后利用两点式写出直线BD的方程
的范围即可. (3)首先根据对称关系设出D点的坐标,然后利用两点式写出直线BD的方程![]() ,根据第一问的计算过程化简直线方程,从而求出直线所过的定点.
,根据第一问的计算过程化简直线方程,从而求出直线所过的定点.
(1)设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,联立曲线方程得:
,联立曲线方程得:
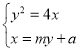
![]()
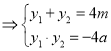
所以![]() .
.
(2) 设![]() 两点的中点坐标为
两点的中点坐标为![]() ,则
,则![]() ,
,
![]() .则
.则![]() ,即AB的垂直平分线为
,即AB的垂直平分线为![]() ,
,
令![]() ,解得
,解得![]() .又
.又![]() ,即
,即![]() ,所以
,所以![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
(3) A关于![]() 轴的对称点为D,则
轴的对称点为D,则![]() ,则直线BD:
,则直线BD:![]() ,整理得:
,整理得:![]() .
.
又![]() =
=![]() .
.
所以直线BD为:![]() =
=![]() ,所以恒过定点
,所以恒过定点![]() .得证.
.得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目