题目内容
设函数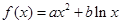 ,其中
,其中 .证明:当
.证明:当 时,函数
时,函数 没有极值点;当
没有极值点;当 时,函数
时,函数 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
当 时,函数
时,函数 没有极值点;
没有极值点;
当 时,
时,
若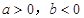 时,函数
时,函数 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为 .
.
若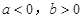 时,函数
时,函数 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为 .
.
解析试题分析:证明:因为 ,所以
,所以 的定义域为
的定义域为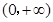 .
.
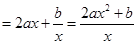 .
.
当 时,如果
时,如果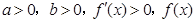 在
在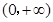 上单调递增;
上单调递增;
如果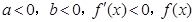 在
在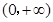 上单调递减.
上单调递减.
所以当 ,函数
,函数 没有极值点.
没有极值点.
当 时,
时,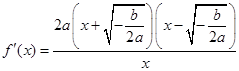
令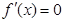 ,得
,得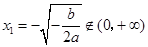 (舍去),
(舍去),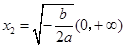 ,
,
当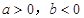 时,
时,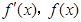 随
随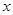 的变化情况如下表:
的变化情况如下表:
从上表可看出,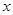
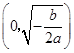
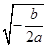
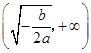

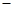
0 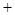

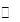
极小值 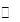
函数 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为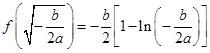 .
.
当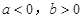 时,
时,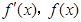 随
随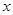 的变化情况如下表:
的变化情况如下表: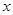
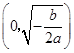
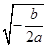
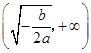

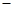
0 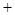

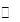
极大值  练习册系列答案
练习册系列答案
寒假生活教育科学出版社系列答案
中考模拟总复习江苏科技出版社系列答案
寒假衔接班寒假提优20天江苏人民出版社系列答案
宏翔文化3年中考2年模拟1年预测系列答案
初中毕业生升学模拟考试系列答案
过好寒假每一天系列答案
寒假作业中国地图出版社系列答案
中考复习攻略南京师范大学出版社系列答案
智多星归类复习测试卷系列答案
智多星模拟加真题测试卷系列答案
相关题目
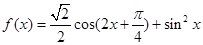 .
.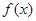 的最小正周期;
的最小正周期;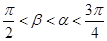 ,且
,且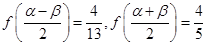 ,求
,求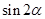 的值.
的值.  ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线 垂直。
垂直。 的值;
的值; 的取值范围。
的取值范围。 满足
满足 (
( +2)=
+2)= 的两实根的平方和为10,
的两实根的平方和为10, 的图象过点(0,3),
的图象过点(0,3), 在
在 上的值域。
上的值域。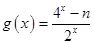 是奇函数,
是奇函数,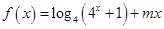 是偶函数。(1)求
是偶函数。(1)求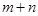 的值;(2)设
的值;(2)设 若
若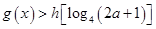 对任意
对任意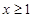 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 上的函数
上的函数 是减函数,且是奇函数,若
是减函数,且是奇函数,若 ,求实数
,求实数 的范围。
的范围。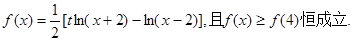
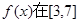 上取得最大值;
上取得最大值;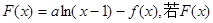 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.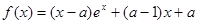 ,
,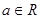 。
。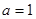 时,求
时,求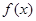 的单调区间;
的单调区间;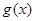 是
是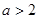 时,在
时,在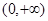 上恰有一个
上恰有一个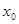 使得
使得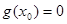 ;
;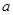 的取值范围,使得对任意的
的取值范围,使得对任意的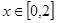 ,恒有
,恒有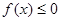 成立。
成立。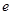 为自然对数的底数。
为自然对数的底数。 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.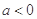 时,解不等式
时,解不等式 ;
;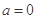 时,求正整数k的值,使方程
时,求正整数k的值,使方程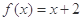 在[k,k+1]上有解;
在[k,k+1]上有解;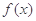 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.