题目内容
(本小题满分14分)
已知函数 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当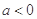 时,解不等式
时,解不等式 ;
;
(2)当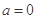 时,求正整数k的值,使方程
时,求正整数k的值,使方程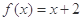 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若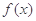 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.
(1)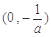 (2)1 (3)
(2)1 (3)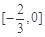
解析试题分析:⑴因为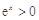 ,所以不等式
,所以不等式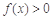 即为
即为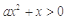 ,
,
又因为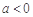 ,所以不等式可化为
,所以不等式可化为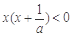 ,
,
所以不等式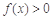 的解集为
的解集为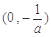 .
.
⑵当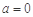 时,方程即为
时,方程即为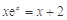 ,由于
,由于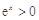 ,所以
,所以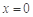 不是方程的解,
不是方程的解,
所以原方程等价于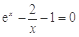 ,令
,令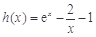 ,
,
因为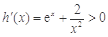 对于
对于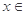
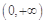 恒成立,
恒成立,
所以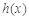 在
在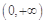 内是单调增函数,
内是单调增函数,
又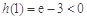 ,
,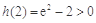 , ,
, ,
所以方程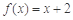 有且只有1个实数根, 在区间
有且只有1个实数根, 在区间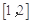 ,
,
所以整数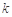 的值为 1.
的值为 1.
⑶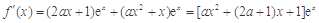 ,
,
① 当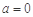 时,
时,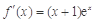 ,
,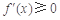 在
在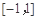 上恒成立,当且仅当
上恒成立,当且仅当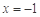 时
时
取等号,故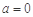 符合要求;
符合要求;
②当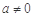 时,令
时,令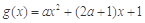 ,因为
,因为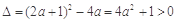 ,
,
所以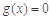 有两个不相等的实数根
有两个不相等的实数根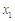 ,
, ,不妨设
,不妨设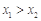 ,
,
因此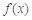 有极大值又有极小值.
有极大值又有极小值.
若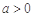 ,因为
,因为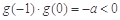 ,所以
,所以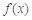 在
在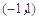 内有极值点,
内有极值点,
故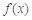 在
在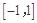 上不单调.
上不单调.
若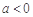 ,可知
,可知 ,
,
因为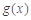 的图象开口向下,要使
的图象开口向下,要使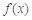 在
在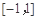 上单调,因为
上单调,因为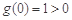 ,
,
必须满足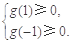 即
即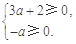 所以
所以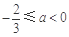 .
.
综上可知,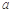 的取值范围是
的取值范围是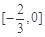 .
.
考点:利用导数求闭区间上函数的最值;函数的单调性与导数的关系.
点评:本题考查的知识是利用导数求闭区间上函数的最值,函数的单调性与导数的关系,熟练掌握导数法在求函数单调性,最值,极值的方法是解答的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
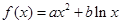 ,其中
,其中 .证明:当
.证明:当 时,函数
时,函数 没有极值点;当
没有极值点;当 时,函数
时,函数
 的单调区间;
的单调区间; 在
在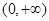 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围; ,求证:
,求证:
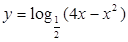
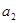 ,
,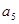 是方程
是方程
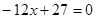 的两根, 数列
的两根, 数列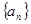 是公差为正的等差数列,数列
是公差为正的等差数列,数列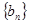 的前
的前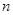 项和为
项和为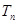 ,且
,且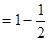
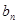
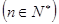 .
.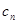 =
=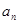
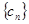 的前
的前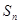 .
.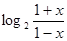 。
。 是定义在R上的奇函数,当
是定义在R上的奇函数,当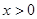 时,
时,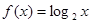
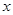 的不等式
的不等式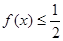
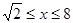 ,求函数
,求函数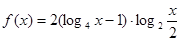 的最大值和最小值
的最大值和最小值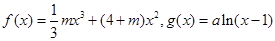 ,其中
,其中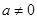 .
.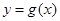 图象恒过定点P,且点P在
图象恒过定点P,且点P在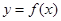 的图象上,求m的值;
的图象上,求m的值;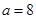 时,设
时,设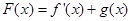 ,讨论
,讨论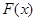 的单调性;
的单调性;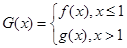 ,曲线
,曲线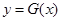 上是否存在两点P、Q,
上是否存在两点P、Q,