题目内容
11.已知命题p:若α为第一象限角,β为第二象限角,则α<β;命题q:在等比数列{an}中,若a1<a2,则数列{an}为递减数列,下列命题为真命题的是( )| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
分析 分别判定命题p,q的真假,再利用复合命题真假的判定方法即可得出.
解答 解:命题p:若α为第一象限角,β为第二象限角,则α<β,是假命题,例如:α=2π+$\frac{π}{6}$,β=$\frac{2π}{3}$;
命题q:在等比数列{an}中,若a1<a2,则数列{an}为递减数列,是假命题,例如:1,-1,1,-1,满足条件,但是不是递减数列.
下列命题为真命题的是(¬p)∧(¬q),
故选:B.
点评 本题考查了复合命题真假的判定方法、象限角、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
6.随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对公务员和教师各抽取了50人进行调查,将调查情况进行整理后制成下表:
附:
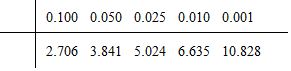
(Ⅰ)求上表中m,n,p的值,并问是否有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为x,求x的分布列和期望.
| 公务员 | 教师 | 合计 | |
| 同意延迟退休 | 40 | n | 70 |
| 不同意延迟退休 | m | 20 | p |
| 合计 | 50 | 50 | 100 |
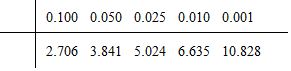
(Ⅰ)求上表中m,n,p的值,并问是否有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为x,求x的分布列和期望.
