题目内容
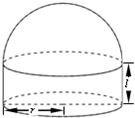 某单位要建造如图所示的仓库,仓库下方是半径为r(m),高为l(m)的圆柱,上方是半球形.按照设计,仓库的体积为定值V(m3).假设该仓库的建造费用仅与表面积有关,圆柱侧面部分每平方米的造价为c元,半球面部分每平方米的造价为2c元,仓库总的建造费用为y元.
某单位要建造如图所示的仓库,仓库下方是半径为r(m),高为l(m)的圆柱,上方是半球形.按照设计,仓库的体积为定值V(m3).假设该仓库的建造费用仅与表面积有关,圆柱侧面部分每平方米的造价为c元,半球面部分每平方米的造价为2c元,仓库总的建造费用为y元.(1)写出y与r的函数关系;
(2)怎样设计仓库,才能使总的建造费用最小?
分析:(1)把半球面的面积用半径r表示出来,由半球的体积与圆柱的体积和等于V得到圆柱的高与底面半径的关系,从而用r表示l,最后把仓库的表面积用含有r的代数式表示,得到建造费用关于r的函数;
(2)利用导函数求极值,也就是最值,同时注意要有实际意义.
(2)利用导函数求极值,也就是最值,同时注意要有实际意义.
解答:解:(1)半球面部分面积为2πr2,
由题意得为πr2l+
πr3=V,∴l=
.
圆柱侧面部分面积为2πrl=2πr•
=
-
πr2,
所以建造费用y=2c•2πr2+c(
-
πr2)=2c(
+
πr2) (r>0).
(2)y′=2c(-
+
πr).
令y′=0得-
+
πr=0,∴r=
.
所以,当仓库的半径r=
时,总的建造费用最少.
由题意得为πr2l+
| 2 |
| 3 |
V-
| ||
| πr2 |
圆柱侧面部分面积为2πrl=2πr•
V-
| ||
| πr2 |
| 2V |
| r |
| 4 |
| 3 |
所以建造费用y=2c•2πr2+c(
| 2V |
| r |
| 4 |
| 3 |
| V |
| r |
| 4 |
| 3 |
(2)y′=2c(-
| V |
| r2 |
| 8 |
| 3 |
令y′=0得-
| V |
| r2 |
| 8 |
| 3 |
| 3 |
| ||
所以,当仓库的半径r=
| 3 |
| ||
点评:本题是根据实际问题选择函数模型题,训练了利用导数求函数的最值,解决实际问题时要注意函数的定义域要有实际意义,此题是中档题.

练习册系列答案
相关题目
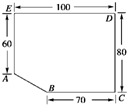
 某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓,问:如何设计才能使公寓占地面积最大?求出最大面积(尺寸单位:m).
某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓,问:如何设计才能使公寓占地面积最大?求出最大面积(尺寸单位:m). 如图所示,某户农民要建造一面靠墙的2间面积相同的矩形猪舍,如果可提供的建造围墙的材料总长为30米,那么宽x(单位:米)为多少时,才能使所建造的猪舍的面积最大,最大面积为多少?
如图所示,某户农民要建造一面靠墙的2间面积相同的矩形猪舍,如果可提供的建造围墙的材料总长为30米,那么宽x(单位:米)为多少时,才能使所建造的猪舍的面积最大,最大面积为多少?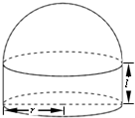 某单位要建造如图所示的仓库,仓库下方是半径为r(m),高为l(m)的圆柱,上方是半球形.按照设计,仓库的体积为定值V(m3).假设该仓库的建造费用仅与表面积有关,圆柱侧面部分每平方米的造价为c元,半球面部分每平方米的造价为2c元,仓库总的建造费用为y元.
某单位要建造如图所示的仓库,仓库下方是半径为r(m),高为l(m)的圆柱,上方是半球形.按照设计,仓库的体积为定值V(m3).假设该仓库的建造费用仅与表面积有关,圆柱侧面部分每平方米的造价为c元,半球面部分每平方米的造价为2c元,仓库总的建造费用为y元.