题目内容
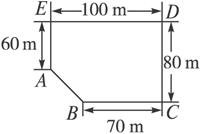
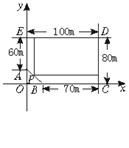
 某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓,问:如何设计才能使公寓占地面积最大?求出最大面积(尺寸单位:m).
某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓,问:如何设计才能使公寓占地面积最大?求出最大面积(尺寸单位:m).分析:设计长方形公寓分三种情况:当一端点在BC上时,只有在B点时长方形BCDB1面积最大;当一端点在EA边上时,只有在A点时长方形AA1DE的面积最大;当一端点在AB边上时,设该点为M,则可构造长方形MNDP,并补出长方形OCDE.由此能求出结果.
解答:解:如图所示,设计长方形公寓分三种情况:
①当一端点在BC上时,只有在B点时长方形BCDB1面积最大,
∴S1=SBCDB1=5600m2.
②当一端点在EA边上时,只有在A点时长方形AA1DE的面积最大,
∴S2=SAA1DE=6 000m2.
③当一端点在AB边上时,设该点为M,则可构造长方形MNDP,并补出长方形OCDE.
设MQ=x(0≤x≤20),∴MP=PQ-MQ=80-x.
又OA=20,OB=30,则
=
,
∴
=
,∴QB=
x,
∴MN=QC=QB+BC=
x+70,
∴S3=SMNDP=MN•MP=(70+
x)•(80-x)
=-
(x-
)2+
,
当x=
时,S3=
.比较S1,S2,S3,得S3最大,
此时MQ=
m,BM=
m,
故当长方形一端点落在AB边上离B点
m处时公寓占地面积最大,最大面积为
m2.

①当一端点在BC上时,只有在B点时长方形BCDB1面积最大,
∴S1=SBCDB1=5600m2.
②当一端点在EA边上时,只有在A点时长方形AA1DE的面积最大,
∴S2=SAA1DE=6 000m2.
③当一端点在AB边上时,设该点为M,则可构造长方形MNDP,并补出长方形OCDE.
设MQ=x(0≤x≤20),∴MP=PQ-MQ=80-x.
又OA=20,OB=30,则
| OA |
| OB |
| MQ |
| QB |
∴
| 2 |
| 3 |
| x |
| QB |
| 3 |
| 2 |
∴MN=QC=QB+BC=
| 3 |
| 2 |
∴S3=SMNDP=MN•MP=(70+
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 50 |
| 3 |
| 18050 |
| 3 |
当x=
| 50 |
| 3 |
| 18050 |
| 3 |
此时MQ=
| 50 |
| 3 |
25
| ||
| 3 |
故当长方形一端点落在AB边上离B点
25
| ||
| 3 |
| 18050 |
| 3 |
点评:本题考查函数在生产生活中的具体运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
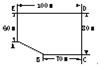 某房地产公司要在荒地ABCDE(如图)上划出一块长方形地面(不改变方位)建造一幢八层的公寓楼,问如何设计才能使公寓占地面积最大?并求出最大面积.(精确到1 m2)
某房地产公司要在荒地ABCDE(如图)上划出一块长方形地面(不改变方位)建造一幢八层的公寓楼,问如何设计才能使公寓占地面积最大?并求出最大面积.(精确到1 m2)