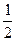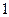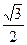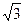题目内容
已知函数f(x)=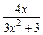 ,x∈[0,2].
,x∈[0,2].
(1)求f(x)的值域;
(2)设a≠0,函数g(x)=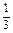 ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
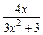 ,x∈[0,2].
,x∈[0,2].(1)求f(x)的值域;
(2)设a≠0,函数g(x)=
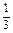 ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.(1)f(x)的值域是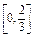 (2)实数a的取值范围是
(2)实数a的取值范围是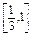
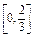 (2)实数a的取值范围是
(2)实数a的取值范围是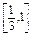
(1)方法一 对函数f(x)求导,f′(x)=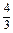 ·
·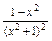 .
.
令f′(x)=0,得x=1或x=-1.
当x∈(0,1)时,f′(x)>0,f(x)在(0,1)上单调递增;
当x∈(1,2)时,f′(x)<0,f(x)在(1,2)上单调递减.又f(0)=0,f(1)=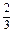 ,f(2)=
,f(2)=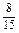 ,
,
∴当x∈[0,2]时,f(x)的值域是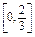 .
.
方法二 当x=0时,f(x)=0;
当x∈(0,2]时,f(x)>0且
f(x)=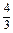 ·
·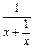 ≤
≤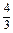 ·
·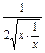 =
=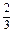 ,
,
当且仅当x=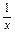 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
∴当x∈[0,2]时,f(x)的值域是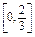 .
.
(2)设函数g(x)在[0,2]上的值域是A.
∵对任意x1∈[0,2],总存在x0∈[0,2],
使f(x1)-g(x0)=0,∴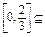 A.
A.
对函数g(x)求导,g′(x)=ax2-a2.
①当x∈(0,2),a<0时,g′(x)<0,
∴函数g(x)在(0,2)上单调递减.
∵g(0)=0,g(2)=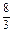 a-2a2<0,
a-2a2<0,
∴当x∈[0,2]时,不满足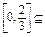 A;
A;
②当a>0时,g′(x)=a(x-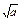 )(x+
)(x+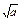 ).
).
令g′(x)=0,得x=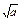 或x=-
或x=-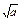 (舍去).
(舍去).
(ⅰ)当x∈[0,2],0<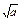 <2时,列表:
<2时,列表:
∵g(0)=0,g(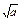 )<0,
)<0,
又∵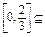 A,∴g(2)=
A,∴g(2)=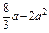 ≥
≥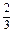 .
.
解得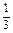 ≤a≤1.
≤a≤1.
(ⅱ)当x∈(0,2),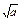 ≥2时,g′(x)<0,
≥2时,g′(x)<0,
∴函数在(0,2)上单调递减,
∵g(0)=0,g(2)=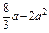 <0,
<0,
∴当x∈[0,2]时,不满足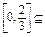 A.
A.
综上,实数a的取值范围是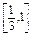 .
.
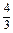 ·
·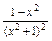 .
.令f′(x)=0,得x=1或x=-1.
当x∈(0,1)时,f′(x)>0,f(x)在(0,1)上单调递增;
当x∈(1,2)时,f′(x)<0,f(x)在(1,2)上单调递减.又f(0)=0,f(1)=
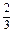 ,f(2)=
,f(2)=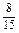 ,
,∴当x∈[0,2]时,f(x)的值域是
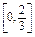 .
.方法二 当x=0时,f(x)=0;
当x∈(0,2]时,f(x)>0且
f(x)=
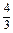 ·
·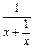 ≤
≤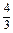 ·
·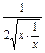 =
=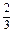 ,
,当且仅当x=
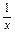 ,即x=1时,“=”成立.
,即x=1时,“=”成立.∴当x∈[0,2]时,f(x)的值域是
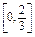 .
.(2)设函数g(x)在[0,2]上的值域是A.
∵对任意x1∈[0,2],总存在x0∈[0,2],
使f(x1)-g(x0)=0,∴
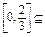 A.
A.对函数g(x)求导,g′(x)=ax2-a2.
①当x∈(0,2),a<0时,g′(x)<0,
∴函数g(x)在(0,2)上单调递减.
∵g(0)=0,g(2)=
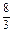 a-2a2<0,
a-2a2<0,∴当x∈[0,2]时,不满足
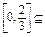 A;
A;②当a>0时,g′(x)=a(x-
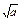 )(x+
)(x+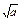 ).
).令g′(x)=0,得x=
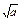 或x=-
或x=-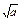 (舍去).
(舍去).(ⅰ)当x∈[0,2],0<
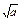 <2时,列表:
<2时,列表:| x | 0 | (0,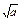 ) ) | 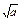 | (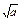 ,2) ,2) | 2 |
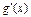 | | - | 0 | + | |
| g(x) | 0 |  | -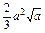 | 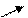 | 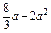 |
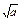 )<0,
)<0,又∵
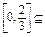 A,∴g(2)=
A,∴g(2)=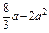 ≥
≥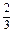 .
.解得
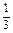 ≤a≤1.
≤a≤1.(ⅱ)当x∈(0,2),
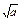 ≥2时,g′(x)<0,
≥2时,g′(x)<0,∴函数在(0,2)上单调递减,
∵g(0)=0,g(2)=
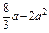 <0,
<0,∴当x∈[0,2]时,不满足
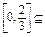 A.
A.综上,实数a的取值范围是
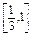 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
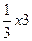 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。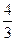 ,试确定b、c的值;
,试确定b、c的值;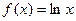
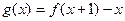 的最大值;
的最大值; 时,求证
时,求证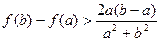 ;
;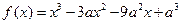 .
.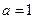 ,求函数
,求函数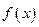 的极值;
的极值;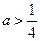 ,且当
,且当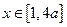 时,
时,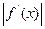
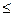 12a恒成立,试确定
12a恒成立,试确定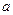 的取值范围.
的取值范围.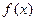 =
=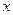 (1-
(1-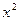 )在[0,1]上的最大值为__________.
)在[0,1]上的最大值为__________.

 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。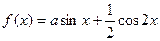 (
(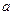 为常数)在
为常数)在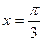 处取得极值,则
处取得极值,则