题目内容
函数f（x）=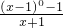
- A.是奇函数但不是偶函数
- B.是偶函数但不是奇函数
- C.既不是奇函数也不是偶函数
- D.既是奇函数，又是偶函数
D
分析：由零指数的意义，化简得f（x）=0．而函数的定义域为{x|x≠±1}关于原点对称，由此可得函数f（x）既是奇函数，又是偶函数．
解答：化简，得f（x）==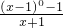
=0
即函数f（x）满足f（-x）=-f（x）且f（-x）=f（x）
∵f（x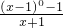）=的定义域为{x|x≠±1}关于原点对称
∴函数既是奇函数，又是偶函数
故选：D
点评：本题判断一个函数的奇偶性，着重考查了零指数的意义和函数奇偶性的定义等知识，属于基础题．
分析：由零指数的意义，化简得f（x）=0．而函数的定义域为{x|x≠±1}关于原点对称，由此可得函数f（x）既是奇函数，又是偶函数．
解答：化简，得f（x）=
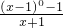==0即函数f（x）满足f（-x）=-f（x）且f（-x）=f（x）
∵f（x）=
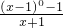的定义域为{x|x≠±1}关于原点对称∴函数既是奇函数，又是偶函数
故选：D
点评：本题判断一个函数的奇偶性，着重考查了零指数的意义和函数奇偶性的定义等知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
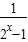+a是奇函数．（1）求常数a的值；（2）判断f（x）的单调性并给出证明．
=（x，1），
=（-1，b-x），函数f（x）=a-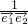
是偶函数．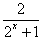
是奇函数（a∈R），
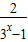是奇函数，求
+a是奇函数，则实数a的值为（ ）
