题目内容
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元;(1)设该农民种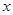 亩水稻,
亩水稻,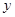 亩花生,利润
亩花生,利润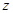 元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
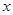 亩水稻,
亩水稻,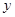 亩花生,利润
亩花生,利润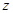 元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?(1)约束条件为
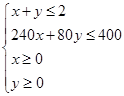 即
即 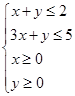 ……4分
……4分
目标函数为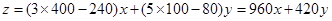 ………7分
………7分
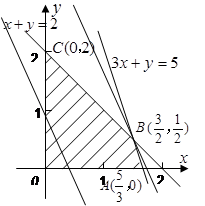
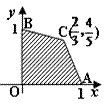
(2)作出可行域如图所示,………………9分
把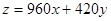 变形为
变形为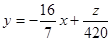 ,得到斜率为
,得到斜率为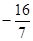 ,在
,在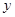 轴上的截距为
轴上的截距为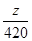 ,随
,随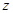 变化的一族平行直线;当直线
变化的一族平行直线;当直线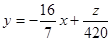 经过可行域上的点B时,截距
经过可行域上的点B时,截距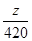 最大,即
最大,即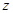 最大。
最大。
解方程组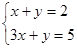 得
得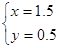 ,即B的坐标是(1.5,0.5) ………12分
,即B的坐标是(1.5,0.5) ………12分
故当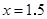 ,
,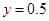 时,
时,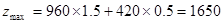 元 ………13分
元 ………13分
答:该农民种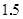 亩水稻,
亩水稻,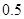 亩花生时,能获得最大利润,最大利润为1650元
亩花生时,能获得最大利润,最大利润为1650元
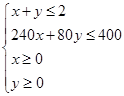 即
即 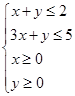 ……4分
……4分目标函数为
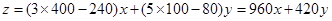 ………7分
………7分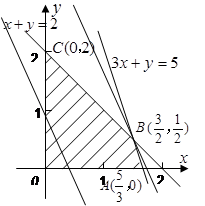
(2)作出可行域如图所示,………………9分
把
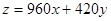 变形为
变形为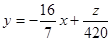 ,得到斜率为
,得到斜率为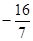 ,在
,在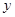 轴上的截距为
轴上的截距为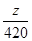 ,随
,随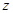 变化的一族平行直线;当直线
变化的一族平行直线;当直线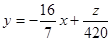 经过可行域上的点B时,截距
经过可行域上的点B时,截距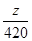 最大,即
最大,即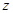 最大。
最大。解方程组
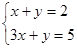 得
得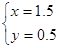 ,即B的坐标是(1.5,0.5) ………12分
,即B的坐标是(1.5,0.5) ………12分故当
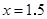 ,
,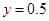 时,
时,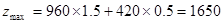 元 ………13分
元 ………13分答:该农民种
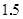 亩水稻,
亩水稻,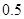 亩花生时,能获得最大利润,最大利润为1650元
亩花生时,能获得最大利润,最大利润为1650元略

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值是
的最大值是  B.
B. C.
C. D.
D.
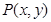 满足
满足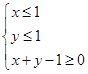 ,点
,点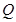 在曲线
在曲线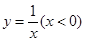 上运动,则
上运动,则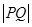 的最小值是( )
的最小值是( )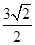
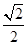
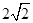
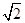
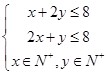 ,目标函数z=3x+y,某学生求得x=
,目标函数z=3x+y,某学生求得x=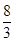 , y=
, y=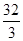 , 这显然不合要求,正确答案应为( )
, 这显然不合要求,正确答案应为( )  月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的
月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的 总量。
总量。 匹需要 / kg
匹需要 / kg 这四个城市之间的客运业务,它们之间的直线距离的部分机票价格如下:
这四个城市之间的客运业务,它们之间的直线距离的部分机票价格如下: 为2000元;
为2000元; 为1600元;
为1600元; 为2500元;
为2500元; 为900元;
为900元; 为1200元,若这家公司规定的机票价格与往返城市间的直线距离成正比,则
为1200元,若这家公司规定的机票价格与往返城市间的直线距离成正比,则 间直线距离的票价为(设这四个城在同一水平面上) ( )
间直线距离的票价为(设这四个城在同一水平面上) ( )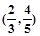 是该目标函数z=ax-y的最优解,则a的取值范围是( )
是该目标函数z=ax-y的最优解,则a的取值范围是( )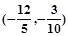

 则下列说法正确的是
则下列说法正确的是  ②
②

