题目内容
已知圆C:x2+y2+x-6y+m=0与直线l:x+2y-3=0.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P,Q两点,O为原点,且OP⊥OQ,求实数m的值
解:(1)将圆的方程配方,
得(x+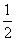 )2+(y-3)2=
)2+(y-3)2= .
.
故有 >0,解得m<
>0,解得m< .
.
将直线l的方程与圆C的方程联立得

消去y,得x2+( )2+x-6×
)2+x-6× +m=0,
+m=0,
整理得5x2+10x+4m-27=0.①
∵直线l与圆C没有公共点,
∴方程①无解,故有Δ=102-4×5(4m-27)<0,解得m>8.
∴m的取值范围是(8, ).
).
(2)设P(x1,y1),Q(x2,y2),
由OP⊥OQ,
得O ·O
·O =0,即x1·x2+y1·y2=0.②
=0,即x1·x2+y1·y2=0.②
由(1)及根与系数的关系得
x1+x2=-2,x1·x2= .③
.③
又∵点P,Q在直线x+2y-3=0上,
∴y1·y2= ·
· =
= [9-3(x1+x2)+x1·x2].
[9-3(x1+x2)+x1·x2].
将③代入上式,得y1·y2= .④
.④
将③④代入②得x1·x2+y1·y2= +
+ =0,解得m=3.
=0,解得m=3.
代入方程①检验得Δ>0成立,∴m=3.

练习册系列答案
相关题目
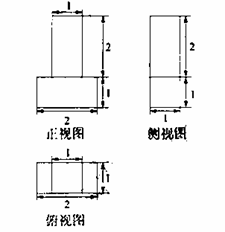
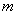 ),则这个几何体的体积为__________
),则这个几何体的体积为__________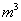
 的前
的前 项和为
项和为 ,且
,且 ,则
,则 _____.
_____.

 ”为真命题的一个充分不必要条件是( )
”为真命题的一个充分不必要条件是( ) B.
B. C.
C. D.
D. 
 ,且
,且 ,则
,则 的值为________.
的值为________. 的定义域为
的定义域为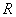 ,若存在常数
,若存在常数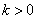 ,使
,使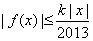 对于一切
对于一切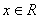 均成立,则称
均成立,则称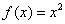 ; ②
; ②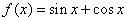 ;
; 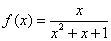 ; ④
; ④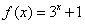 。其中
。其中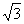 ,则异面直线AD,BC所成的角为( )
,则异面直线AD,BC所成的角为( )