题目内容
从一块圆心角为
，半径为R的扇形钢板上切割一块矩形钢板，请问怎样设计切割方案，才能使矩形面积最大？并说明理由．
| 2π |
| 3 |
考点：基本不等式,扇形面积公式
专题：不等式的解法及应用
分析：对甲种裁法分析设OE=a，EF=b，则得出面积，利用基本不等式求最值的方法求出最大面积；对乙种裁法分析设∠COB=θ，利用三角函数表示出长为2Rsin（60°-θ），用正弦定理，表示BC，进而表示出面积，比较看哪个面积大即可．
解答：
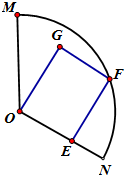
解：方案一：GF∥ON
设OE=a，EF=b，S矩形OEFG=OE×EF=ab≤
，a2+b2=R2
当a=b时，S矩形OEFG的最大值为
．
方案二：AB∥MN
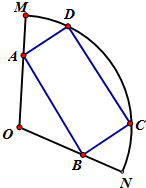
设∠COB=θ，(0＜θ＜
)AB=2OCsin(
-θ)=2Rsin(
-θ)
在△BOC中运用正弦定理，
=
∠OBC=
，
=
，BC=
，
S矩形ABCD=AB×CD=
2Rsin(
-θ)，
令y=sinθsin(
-θ)=-
[cos(θ+
-θ)-cos(θ-
+θ)]=
cos(2θ-
)-
，当θ=
时，ymax=
，
S矩形OEFG的最大值
=
而
＞
故选方案二才能使矩形面积最大．
设OE=a，EF=b，S矩形OEFG=OE×EF=ab≤
| a2+b2 |
| 2 |
当a=b时，S矩形OEFG的最大值为
| R2 |
| 2 |
方案二：AB∥MN
设∠COB=θ，(0＜θ＜
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
在△BOC中运用正弦定理，
| OC |
| sin∠OBC |
| BC |
| sin∠BOC |
| 2π |
| 3 |
| R | ||
sin
|
| BC |
| sinθ |
| 2Rsinθ | ||
|
S矩形ABCD=AB×CD=
| 2Rsinθ | ||
|
| π |
| 3 |
令y=sinθsin(
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 4 |
| π |
| 6 |
| 1 |
| 4 |
S矩形OEFG的最大值
| R2 | ||
|
| ||
| 3 |
而
| ||
| 3 |
| R2 |
| 2 |
点评：考查学生根据实际问题选择函数类型的能力，以及运用两角和与差的正弦函数的能力，求正弦函数最值的能力．
练习册系列答案
相关题目