题目内容
16.已知a为实数,函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).(1)求g(a)的解析式;
(2)若关于a的方程g(a)-3+b=0有两解,求实数b的取值范围.
分析 (1)分类讨论以确定函数的单调性及去绝对值号,从而确定g(a)的解析式;
(2)作函数g(x)与y=3-b的图象,从而可得3-b>1-(2$\sqrt{2}$-2)=3-2$\sqrt{2}$,从而解得.
解答 解:(1)①当a≤0时,f(x)=x2-ax在区间[0,1]上是增函数,
∴g(a)=f(1)=1-a,
②当0<a<1时,
f(x)在[0,$\frac{a}{2}$)上是增函数,在[$\frac{a}{2}$,a)上是减函数,在[a,1]上是增函数;
而f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,f(1)=1-a,
∵f($\frac{a}{2}$)-f(1)=$\frac{{a}^{2}}{4}$+a-1,
故当a∈(0,2$\sqrt{2}$-2]时,f($\frac{a}{2}$)≤f(1),g(a)=f(1)=1-a,
当a∈(2$\sqrt{2}$-2,1)时,f($\frac{a}{2}$)>f(1),g(a)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,
③当1≤a<2时,f(x)在[0,$\frac{a}{2}$)上是增函数,在[$\frac{a}{2}$,1]上是减函数,
故g(a)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,
④当a≥2时,f(x)在[0,1]上是增函数,
故g(a)=f(1)=a-1,
综上所述,
g(a)=$\left\{\begin{array}{l}{1-a,a≤2\sqrt{2}-2}\\{\frac{{a}^{2}}{4},2\sqrt{2}-2<a<2}\\{a-1,a≥2}\end{array}\right.$,
(2)作函数g(x)与y=3-b的图象如下,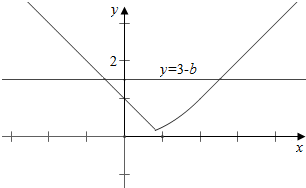 ,
,
结合图象可知,
3-b>1-(2$\sqrt{2}$-2)=3-2$\sqrt{2}$,
故b<2$\sqrt{2}$.
点评 本题考查了分类讨论的思想应用及分段函数的应用,同时考查了数形结合的思想应用.

| A. | 1+i | B. | l-i | C. | -l+i | D. | -l-i |
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$或2 | D. | 2 |
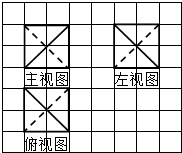
| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
| A. | 12,3 | B. | -12,-3 | C. | 12,-3 | D. | -12,3 |